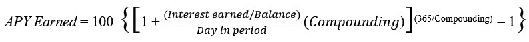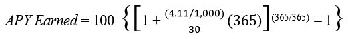The annual percentage yield
earned for periodic statements under section 1030.6(a) is an annualized
rate that reflects the relationship between the amount of interest
actually earned on the consumer’s account during the statement period
and the average daily balance in the account for the statement period.
Pursuant to section 1030.6(b), however, if an institution uses the
average daily balance method and calculates interest for a period
other than the statement period, the annual percentage yield earned
shall reflect the relationship between the amount of interest earned
and the average daily balance in the account for that other period.
The annual percentage yield earned shall be calculated by using the
following formulas (“APY Earned” is used for convenience in the formulas):
A. General Formula APY Earned = 100 [(1 + Interest
earned/Balance)(365/Days in period) - 1]
“Balance” is the average daily balance
in the account for the period.
“Interest earned” is the actual amount of interest earned
on the account for the period.
“Days in period” is the actual number of days for the
period.
Examples:
(1) Assume an institution calculates interest
for the statement period (and uses either the daily balance or the
average daily balance method), and the account has a balance of $1,500
for 15 days and a balance of $500 for the remaining 15 days of a 30-day
statement period. The average daily balance for the period is $1,000.
The interest earned (under either balance computation method) is $5.25
during the period. The annual percentage yield earned (using the formula
above) is 6.58%:
APY Earned = 100 [(1 + 5.25/1,000)(365/30) - 1]
APY Earned = 6.58%
(2) Assume an institution calculates interest
on the average daily balance for the calendar month and provides periodic
statements that cover the period from the 16th of one month to the
15th of the next month. The account has a balance of $2,000 September
1 through September 15 and a balance of $1,000 for the remaining 15
days of September. The average daily balance for the month of September
is $1,500, which results in $6.50 in interest earned for the month.
The annual percentage yield earned for the month of September would
be shown on the periodic statement covering September 16 through October
15. The annual percentage yield earned (using the formula above) is
5.40%:
APY Earned = 100 [(6.50/1,500)(365/30) - 1]
APY Earned = 5.40%
(3) Assume an institution calculates interest
on the average daily balance for a quarter (for example, the calendar
months of September through November), and provides monthly periodic
statements covering calendar months. The account has a balance of
$1,000 throughout the 30 days of September, a balance of $2,000 throughout
the 31 days of October, and a balance of $3,000 throughout the 30
days of November. The average daily balance for the quarter is $2,000,
which results in $21 in interest earned for the quarter. The annual
percentage yield earned would be shown on the periodic statement for
November. The annual percentage yield earned (using the formula above)
is 4.28%:
APY Earned = 100 [(1 + 21/2,000)(365/91) - 1]
APY Earned = 4.28%
B. Special Formula for Use Where Periodic
Statement Is Sent More Often Than the Period for Which Interest Is
Compounded Institutions that use the
daily balance method to accrue interest and that issue periodic statements
more often than the period for which interest is compounded shall
use the following special formula:
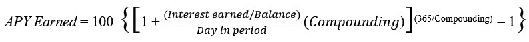
$$
\begin{align*}
APY Earned = 100 \text{ } \Bigg\{\Bigg[ 1 + \frac{(\textit{Interest earned/Balance})}{\textit{Day in period}} (Compounding) \Bigg]^{(\text{365/Compounding})} - 1 \Bigg\}
\end{align*}
$$
The following definition applies for use
in this formula (all other terms are defined under part II):
“Compounding” is the number of days
in each compounding period.
Assume an institution calculates interest for the statement
period using the daily balance method, pays a 5.00% interest rate,
compounded annually, and provides periodic statements for each monthly
cycle. The account has a daily balance of $1,000 for a 30-day statement
period. The interest earned is $4.11 for the period, and the annual
percentage yield earned (using the special formula above) is 5.00%:
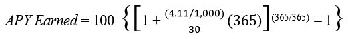
$$
\begin{align*}
APY Earned = 100 \text{ } \Bigg\{\Bigg[ 1 + \frac{(4.11/1,000)}{30} (365) \Bigg]^{(\text{365/365})} - 1 \Bigg\}
\end{align*}
$$
APY Earned = 5.00%