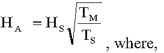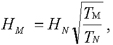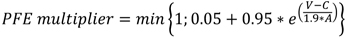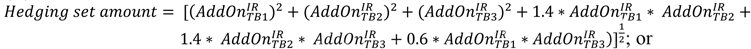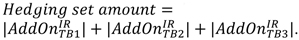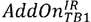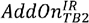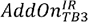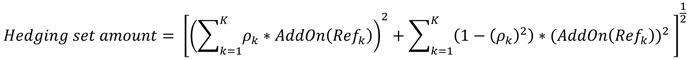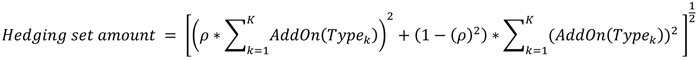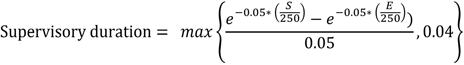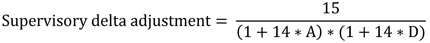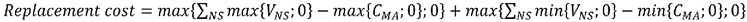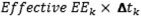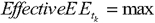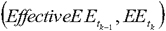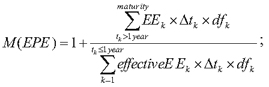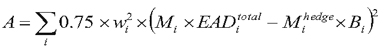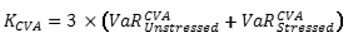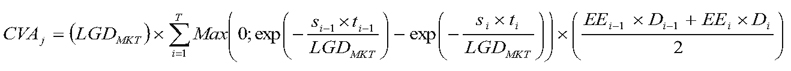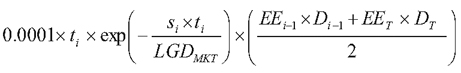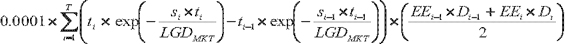(1) Instead of an LGD estimation methodology,
a Board-regulated institution may use the following methodologies
to recognize the benefits of financial collateral in mitigating the
counterparty credit risk of repo-style transactions, eligible margin
loans, collateralized OTC derivative contracts and single product
netting sets of such transactions, and to recognize the benefits of
any collateral in mitigating the counterparty credit risk of repo-style
transactions that are included in a Board-regulated institution’s
VaR-based measure under subpart F of this part:
(i) The
collateral haircut approach set forth in paragraph (b)(2) of this
section;
(ii) The
internal models methodology set forth in paragraph (d) of this section;
and
(iii) For single
product netting sets of repo-style transactions and eligible margin
loans, the simple VaR methodology set forth in paragraph (b)(3) of
this section.
(2) A Board-regulated institution may use
any combination of the three methodologies for collateral recognition;
however, it must use the same methodology for transactions in the
same category.
(3) A
Board-regulated institution must use the methodology in paragraph
(c) of this section, or with prior written approval of the Board,
the internal model methodology in paragraph (d) of this section, to
calculate EAD for an OTC derivative contract or a set of OTC derivative
contracts subject to a qualifying master netting agreement. To estimate
EAD for qualifying cross-product master netting agreements, a Board-regulated
institution may only use the internal models methodology in paragraph
(d) of this section.
(4) A Board-regulated institution must also use the methodology in
paragraph (e) of this section to calculate the risk-weighted asset
amounts for CVA for OTC derivatives.
(1) General. A Board-regulated institution may recognize the credit risk mitigation
benefits of financial collateral that secures an eligible margin loan,
repo-style transaction, or single-product netting set of such transactions
by factoring the collateral into its LGD estimates for the exposure.
Alternatively, a Board-regulated institution may estimate an unsecured
LGD for the exposure, as well as for any repo-style transaction that
is included in the Board-regulated institution’s VaR-based measure
under subpart F of this part, and determine the EAD of the exposure
using:
(i) The collateral haircut approach
described in paragraph (b)(2) of this section;
(ii) For netting sets only,
the simple VaR methodology described in paragraph (b)(3) of this section;
or
(iii) The internal
models methodology described in paragraph (d) of this section.
(2) Collateral haircut approach.
(i) EAD equation. A Board-regulated institution
may determine EAD for an eligible margin loan, repo-style transaction,
or netting set by setting EAD equal to max {0, [(∑E − ∑C) + ∑(Es × Hs) + ∑(Efx × Hfx)]},
where:
(A) ∑E equals the value of the exposure (the
sum of the current fair values of all instruments, gold, and cash
the Board-regulated institution has lent, sold subject to repurchase,
or posted as collateral to the counterparty under the transaction
(or netting set));
(B)
∑C equals the value of the collateral (the sum of the current fair
values of all instruments, gold, and cash the Board-regulated institution
has borrowed, purchased subject to resale, or taken as collateral
from the counterparty under the transaction (or netting set));
(C) Es equals
the absolute value of the net position in a given instrument or in
gold (where the net position in a given instrument or in gold equals
the sum of the current fair values of the instrument or gold the Board-regulated
institution has lent, sold subject to repurchase, or posted as collateral
to the counterparty minus the sum of the current fair values of that
same instrument or gold the Board-regulated institution has borrowed,
purchased subject to resale, or taken as collateral from the counterparty);
(D) Hs equals
the market price volatility haircut appropriate to the instrument
or gold referenced in Es;
(E) Efx equals the absolute value
of the net position of instruments and cash in a currency that is
different from the settlement currency (where the net position in
a given currency equals the sum of the current fair values of any
instruments or cash in the currency the Board-regulated institution
has lent, sold subject to repurchase, or posted as collateral to the
counterparty minus the sum of the current fair values of any instruments
or cash in the currency the Board-regulated institution has borrowed,
purchased subject to resale, or taken as collateral from the counterparty);
and
(F) Hfx equals
the haircut appropriate to the mismatch between the currency referenced
in Efx and the settlement currency.
(ii) Standard supervisory haircuts.
(A) Under the
standard supervisory haircuts approach:
(1) A Board-regulated institution must use the haircuts for
market price volatility (Hs) in Table 1 to section 217.132,
as adjusted in certain circumstances as provided in paragraphs (b)(2)(ii)(A)(3) and (4) of this section;
Table 1 to section
217.132—Standard supervisory market price volatility haircuts
| |
Haircut (in percent) assigned based on: |
Investment grade securitization exposures
(in percent) |
| Residual maturity |
Sovereign issuers risk weight under section 217.1322 (in percent) |
Non-sovereign issuers risk weight under section
217.132 (in percent) |
| Less than or
equal to 1 year |
0.5 |
1.0 |
15.0 |
1.0 |
2.0 |
4.0 |
4.0 |
| Greater than
1 year and less than or equal to 5 years |
2.0 |
3.0 |
15.0 |
4.0 |
6.0 |
8.0 |
12.0 |
| Greater than
5 years |
4.0 |
6.0 |
15.0 |
8.0 |
12.0 |
16.0 |
24.0 |
| Main index equities
(including convertible bonds) and gold |
15.0 |
| Other publicly traded
equities (including convertible bonds) |
25.0 |
| Mutual funds |
Highest
haircut applicable to any security in which the fund can invest. |
| Cash collateral held |
Zero |
| Other exposure
types |
25.0 |
1 The market price volatility haircuts in Table 1 to section
217.132 are based on a 10 business-day holding period.
2 Includes
a foreign PSE that receives a zero percent risk weight.
(2) For currency mismatches,
a Board-regulated institution must use a haircut for foreign exchange
rate volatility (Hfx) of 8 percent, as adjusted in certain
circumstances as provided in paragraphs (b)(2)(ii)(A)(3) and
(4) of this section.
(3) For repo-style transactions and client-facing derivative
transactions, a Board-regulated institution may multiply the supervisory
haircuts provided in paragraphs (b)(2)(ii)(A)(1) and (2) of this section by the square root of ½ (which equals 0.707107).
If the Board-regulated institution determines that a longer holding
period is appropriate for client-facing derivative transactions, then
it must use a larger scaling factor to adjust for the longer holding
period pursuant to paragraph (b)(2)(ii)(A)(6) of this section.
(4) A Board-regulated
institution must adjust the supervisory haircuts upward on the basis
of a holding period longer than ten business days (for eligible margin
loans) or five business days (for repo-style transactions), using
the formula provided in paragraph (b)(2)(ii)(A)(6) of this
section where the conditions in this paragraph (b)(2)(ii)(A)(4) apply. If the number of trades in a netting set exceeds 5,000 at
any time during a quarter, a Board-regulated institution must adjust
the supervisory haircuts upward on the basis of a minimum holding
period of twenty business days for the following quarter (except when
a Board-regulated institution is calculating EAD for a cleared transaction
under section 217.133). If a netting set contains one or more trades
involving illiquid collateral, a Board-regulated institution must
adjust the supervisory haircuts upward on the basis of a minimum holding
period of twenty business days. If over the two previous quarters
more than two margin disputes on a netting set have occurred that
lasted longer than the holding period, then the Board-regulated institution
must adjust the supervisory haircuts upward for that netting set on
the basis of a minimum holding period that is at least two times the
minimum holding period for that netting set.
(5)(i) A Board-regulated
institution must adjust the supervisory haircuts upward on the basis
of a holding period longer than ten business days for collateral
associated with derivative contracts (five business days for client-facing
derivative contracts) using the formula provided in paragraph (b)(2)(ii)(A)(6) of this section where the conditions in this paragraph (b)(2)(ii)(A)(5)(i) apply. For collateral associated with a derivative
contract that is within a netting set that is composed of more than
5,000 derivative contracts that are not cleared transactions, a Board-regulated
institution must use a minimum holding period of twenty business days.
If a netting set contains one or more trades involving illiquid collateral
or a derivative contract that cannot be easily replaced, a Board-regulated
institution must use a minimum holding period of twenty business days.
(ii) Notwithstanding
paragraph (b)(2)(ii)(A)(1) or (3) or (b)(2)(ii)(A)(5)(i) of this section, for collateral associated with
a derivative contract in a netting set under which more than two margin
disputes that lasted longer than the holding period occurred during
the two previous quarters, the minimum holding period is twice the
amount provided under paragraph (b)(2)(ii)(A)(1) or (3) or (b)(2)(ii)(A)(5)(i) of this section.
(6) A Board-regulated
institution must adjust the standard supervisory haircuts upward,
pursuant to the adjustments provided in paragraphs (b)(2)(ii)(A)(3) through (5) of this section, using the following formula:
Figure 1. DISPLAY EQUATION
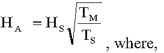
$$
H_{A}=H_{S}\sqrt[]{\frac{T_{M}}{T_{S}}}
$$
Where:
TM equals a holding
period of longer than 10 business days for eligible margin loans and
derivative contracts other than client-facing derivative transactions
or longer than 5 business days for repo-style transactions and client-facing
derivative transactions;
HS equals the standard supervisory haircut; and
TS equals 10 business
days for eligible margin loans and derivative contracts other than
client-facing derivative transactions or 5 business days for repo-style
transactions and client-facing derivative transactions.
(7) If the instrument
a Board-regulated institution has lent, sold subject to repurchase,
or posted as collateral does not meet the definition of financial
collateral, the Board-regulated institution must use a 25.0 percent
haircut for market price volatility (HS).
(iii) Own internal estimates for haircuts. With
the prior written approval of the Board, a Board-regulated institution
may calculate haircuts (Hs and Hfx) using its
own internal estimates of the volatilities of market prices and foreign
exchange rates.
(A) To receive Board approval to use its own
internal estimates, a Board-regulated institution must satisfy the
following minimum quantitative standards:
(1) A Board-regulated institution must use a 99th percentile
one-tailed confidence interval.
(2) The minimum holding period for
a repo-style transaction is five business days and for an eligible
margin loan is ten business days except for transactions or netting
sets for which paragraph (b)(2)(iii)(A)(3) of this section
applies. When a Board-regulated institution calculates an own-estimates
haircut on a TN -day holding period, which is different
from the minimum holding period for the transaction type, the applicable
haircut (HM) is calculated using the following square root
of time formula:
Figure 2. DISPLAY EQUATION
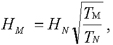
$$
H_M = H_N \sqrt{\frac{T_M}{T_N}} \text{ , }
$$
where
(i) TM equals 5 for repo-style
transactions and 10 for eligible margin loans;
(ii) TN equals the holding
period used by the Board-regulated institution to derive HN; and
(iii) HN equals the haircut based on the holding period TN.
(3) If the number of trades in a netting set exceeds 5,000 at
any time during a quarter, a Board-regulated institution must calculate
the haircut using a minimum holding period of twenty business days
for the following quarter (except when a Board-regulated institution
is calculating EAD for a cleared transaction under section 217.133).
If a netting set contains one or more trades involving illiquid collateral
or an OTC derivative that cannot be easily replaced, a Board-regulated
institution must calculate the haircut using a minimum holding period
of twenty business days. If over the two previous quarters more than
two margin disputes on a netting set have occurred that lasted more
than the holding period, then the Board-regulated institution must
calculate the haircut for transactions in that netting set on the
basis of a holding period that is at least two times the minimum holding
period for that netting set.
(4) A Board-regulated institution
is required to calculate its own internal estimates with inputs calibrated
to historical data from a continuous 12-month period that reflects
a period of significant financial stress appropriate to the security
or category of securities.
(5) A Board-regulated institution must have policies and procedures
that describe how it determines the period of significant financial
stress used to calculate the Board-regulated institution’s own internal
estimates for haircuts under this section and must be able to provide
empirical support for the period used. The Board-regulated institution
must obtain the prior approval of the Board for, and notify the Board
if the Board-regulated institution makes any material changes to,
these policies and procedures.
(6) Nothing in this section prevents
the Board from requiring a Board-regulated institution to use a different
period of significant financial stress in the calculation of own internal
estimates for haircuts.
(7) A Board-regulated institution must update its data sets
and calculate haircuts no less frequently than quarterly and must
also reassess data sets and haircuts whenever market prices change
materially.
(B) With respect to debt securities that are investment grade, a
Board-regulated institution may calculate haircuts for categories
of securities. For a category of securities, the Board-regulated institution
must calculate the haircut on the basis of internal volatility estimates
for securities in that category that are representative of the securities
in that category that the Board-regulated institution has lent, sold
subject to repurchase, posted as collateral, borrowed, purchased subject
to resale, or taken as collateral. In determining relevant categories,
the Board-regulated institution must at a minimum take into account:
(1) The type of issuer of the security;
(2) The credit quality
of the security;
(3) The maturity of the security; and
(4) The interest rate sensitivity
of the security.
(C) With respect to debt securities that are
not investment grade and equity securities, a Board-regulated institution
must calculate a separate haircut for each individual security.
(D) Where an exposure or
collateral (whether in the form of cash or securities) is denominated
in a currency that differs from the settlement currency, the Board-regulated
institution must calculate a separate currency mismatch haircut for
its net position in each mismatched currency based on estimated volatilities
of foreign exchange rates between the mismatched currency and the
settlement currency.
(E)
A Board-regulated institution’s own estimates of market price and
foreign exchange rate volatilities may not take into account the correlations
among securities and foreign exchange rates on either the exposure
or collateral side of a transaction (or netting set) or the correlations
among securities and foreign exchange rates between the exposure and
collateral sides of the transaction (or netting set).
(3) Simple VaR methodology. With the prior
written approval of the Board, a Board-regulated institution may estimate
EAD for a netting set using a VaR model that meets the requirements
in paragraph (b)(3)(iii) of this section. In such event, the Board-regulated
institution must set EAD equal to max {0, [(ΣE− ΣC) + PFE]}, where:
(i) ∑E equals the value of the exposure (the sum of the current fair
values of all instruments, gold, and cash the Board-regulated institution
has lent, sold subject to repurchase, or posted as collateral to the
counterparty under the netting set);
(ii) ∑C equals the value of the collateral
(the sum of the current fair values of all instruments, gold, and
cash the Board-regulated institution has borrowed, purchased subject
to resale, or taken as collateral from the counterparty under the
netting set); and
(iii) PFE (potential future exposure) equals the Board-regulated
institution’s empirically based best estimate of the 99th percentile,
one-tailed confidence interval for an increase in the value of (∑E − ∑C)
over a five-business-day holding period for repo-style transactions,
or over a ten-business-day holding period for eligible margin loans
except for netting sets for which paragraph (b)(3)(iv) of this section
applies using a minimum one-year historical observation period of price
data representing the instruments that the Board-regulated institution
has lent, sold subject to repurchase, posted as collateral, borrowed,
purchased subject to resale, or taken as collateral. The Board-regulated
institution must validate its VaR model by establishing and maintaining
a rigorous and regular backtesting regime.
(iv) If the number of trades in a netting
set exceeds 5,000 at any time during a quarter, a Board-regulated
institution must use a twenty-business-day holding period for the
following quarter (except when a Board-regulated institution is calculating
EAD for a cleared transaction under section 217.133). If a netting
set contains one or more trades involving illiquid collateral, a Board-regulated
institution must use a twenty-business-day holding period. If over
the two previous quarters more than two margin disputes on a netting
set have occurred that lasted more than the holding period, then the
Board-regulated institution must set its PFE for that netting set
equal to an estimate over a holding period that is at least two times
the minimum holding period for that netting set.
(1) Options for
determining EAD. A Board-regulated institution must determine
the EAD for a derivative contract using the standardized approach
for counterparty credit risk (SA-CCR) under paragraph (c)(5) of this
section or using the internal models methodology described in paragraph
(d) of this section. If a Board-regulated institution elects to use
SA-CCR for one or more derivative contracts, the exposure amount determined
under SA-CCR is the EAD for the derivative contract or derivatives
contracts. A Board-regulation institution must use the same methodology
to calculate the exposure amount for all its derivative contracts
and may change its election only with prior approval of the Board.
A Board-regulated institution may reduce the EAD calculated according
to paragraph (c)(5) of this section by the credit valuation adjustment
that the Board-regulated institution has recognized in its balance
sheet valuation of any derivative contracts in the netting set. For
purposes of this paragraph (c)(1), the credit valuation adjustment does
not include any adjustments to common equity tier 1 capital attributable
to changes in the fair value of the Board-regulated institution’s
liabilities that are due to changes in its own credit risk since the
inception of the transaction with the counterparty.
(2) Definitions. For purposes of this paragraph (c) of this section, the following
definitions apply:
(i) End date means the last date
of the period referenced by an interest rate or credit derivative
contract or, if the derivative contract references another instrument,
by the underlying instrument, except as otherwise provided in paragraph
(c) of this section.
(ii) Start date means the first date of the period referenced
by an interest rate or credit derivative contract or, if the derivative
contract references the value of another instrument, by underlying
instrument, except as otherwise provided in paragraph (c) of this
section.
(iii) Hedging set means:
(A) With respect to interest rate derivative
contracts, all such contracts within a netting set that reference
the same reference currency;
(B) With respect to exchange rate derivative contracts, all such
contracts within a netting set that reference the same currency pair;
(C) With respect to credit
derivative contract, all such contracts within a netting set;
(D) With respect to equity derivative
contracts, all such contracts within a netting set;
(E) With respect to a commodity derivative
contract, all such contracts within a netting set that reference one
of the following commodity categories: Energy, metal, agricultural,
or other commodities;
(F) With respect to basis derivative contracts, all such contracts
within a netting set that reference the same pair of risk factors
and are denominated in the same currency; or
(G) With respect to volatility derivative
contracts, all such contracts within a netting set that reference
one of interest rate, exchange rate, credit, equity, or commodity
risk factors, separated according to the requirements under paragraphs
(c)(2)(iii)(A) through (E) of this section.
(H) If the risk of a derivative contract materially
depends on more than one of interest rate, exchange rate, credit,
equity, or commodity risk factors, the Board may require a Board-regulated
institution to include the derivative contract in each appropriate
hedging set under paragraphs (c)(1)(iii)(A) through (E) of this section.
(3) Credit derivatives. Notwithstanding
paragraphs (c)(1) and (c)(2) of this section:
(i) A Board-regulated
institution that purchases a credit derivative that is recognized
under section 217.134 or section 217.135 as a credit risk mitigant
for an exposure that is not a covered position under subpart F of
this part is not required to calculate a separate counterparty credit
risk capital requirement under this section so long as the Board-regulated
institution does so consistently for all such credit derivatives and
either includes or excludes all such credit derivatives that are subject
to a master netting agreement from any measure used to determine counterparty
credit risk exposure to all relevant counterparties for risk-based
capital purposes.
(ii) A Board-regulated institution that is the protection provider
in a credit derivative must treat the credit derivative as a wholesale
exposure to the reference obligor and is not required to calculate
a counterparty credit risk capital requirement for the credit derivative
under this section, so long as it does so consistently for all such
credit derivatives and either includes all or excludes all such credit
derivatives that are subject to a master netting agreement from any
measure used to determine counterparty credit risk exposure to all
relevant counterparties for risk-based capital purposes (unless the
Board-regulated institution is treating the credit derivative as a
covered position under subpart F of this part, in which case the Board-regulated
institution must calculate a supplemental counterparty credit risk
capital requirement under this section).
(4) Equity derivatives. A Board-regulated institution must treat
an equity derivative contract as an equity exposure and compute a
risk-weighted asset amount for the equity derivative contract under
sections 217.151-217.155 (unless the Board-regulated institution is
treating the contract as a covered position under subpart F of this
part). In addition, if the Board-regulated institution is treating
the contract as a covered position under subpart F of this part, and
under certain other circumstances described in section 217.155, the
Board-regulated institution must also calculate a risk-based capital
requirement for the counterparty credit risk of an equity derivative
contract under this section.
(5) Exposure
amount.
(i) The exposure amount of a netting
set, as calculated under paragraph (c) of this section, is equal to
1.4 multiplied by the sum of the replacement cost of the netting set,
as calculated under paragraph (c)(6) of this section, and the potential
future exposure of the netting set, as calculated under paragraph
(c)(7) of this section.
(ii) Notwithstanding the requirements of paragraph (c)(5)(i) of this
section, the exposure amount of a netting set subject to a variation
margin agreement, excluding a netting set that is subject to a variation
margin agreement under which the counterparty to the variation margin
agreement is not required to post variation margin, is equal to the
lesser of the exposure amount of the netting set calculated under
paragraph (c)(5)(i) of this section and the exposure amount of the
netting set calculated under paragraph (c)(5)(i) of this section as
if the netting set were not subject to a variation margin agreement.
(iii) Notwithstanding
the requirements of paragraph (c)(5)(i) of this section, the exposure
amount of a netting set that consists of only sold options in which
the premiums have been fully paid by the counterparty to the options
and where the options are not subject to a variation margin agreement
is zero.
(iv) Notwithstanding
the requirements of paragraph (c)(5)(i) of this section, the exposure
amount of a netting set in which the counterparty is a commercial
end-user is equal to the sum of replacement cost, as calculated under
paragraph (c)(6) of this section, and the potential future exposure
of the netting set, as calculated under paragraph (c)(7) of this section.
(v) For purposes of
the exposure amount calculated under paragraph (c)(5)(i) of this section
and all calculations that are part of that exposure amount, a Board-regulated
institution may elect to treat a derivative contract that is a cleared
transaction that is not subject to a variation margin agreement as
one that is subject to a variation margin agreement, if the derivative
contract is subject to a requirement that the counterparties make
daily cash payments to each other to account for changes in the fair
value of the derivative contract and to reduce the net position of
the contract to zero. If a Board-regulated institution makes an election
under this paragraph (c)(5)(v) for one derivative contract, it must
treat all other derivative contracts within the same netting set that
are eligible for an election under this paragraph (c)(5)(v) as derivative
contracts that are subject to a variation margin agreement.
(vi) For purposes of the
exposure amount calculated under paragraph (c)(5)(i) of this section
and all calculations that are part of that exposure amount, a Board-regulated
institution may elect to treat a credit derivative contract, equity
derivative contract, or commodity derivative contract that references
an index as if it were multiple derivative contracts each referencing
one component of the index.
(6) Replacement
cost of a netting set.
(i) Netting
set subject to a variation margin agreement under which the
counterparty must post variation margin. The replacement cost
of a netting set subject to a variation margin agreement, excluding
a netting set that is subject to a variation margin agreement under
which the counterparty is not required to post variation margin, is
the greater of:
(A) The sum of the fair values (after excluding
any valuation adjustments) of the derivative contracts within the
netting set less the sum of the net independent collateral amount
and the variation margin amount applicable to such derivative contracts;
(B) The sum of the variation
margin threshold and the minimum transfer amount applicable to the
derivative contracts within the netting set less the net independent
collateral amount applicable to such derivative contracts; or
(C) Zero.
(ii) Netting sets not subject to a variation margin agreement under which
the counterparty must post variation margin. The replacement
cost of a netting set that is not subject to a variation margin agreement
under which the counterparty must post variation margin to the Board-regulated
institution is the greater of:
(A) The sum of the fair values
(after excluding any valuation adjustments) of the derivative contracts
within the netting set less the sum of the net independent collateral
amount and variation margin amount applicable to such derivative contracts;
or
(B) Zero.
(iii) Multiple netting sets subject to a single variation
margin agreement. Notwithstanding paragraphs (c)(6)(i) and (ii)
of this section, the replacement cost for multiple netting sets subject
to a single variation margin agreement must be calculated according
to paragraph (c)(10)(i) of this section.
(iv) Netting
set subject to multiple variation margin agreements or a hybrid netting
set. Notwithstanding paragraphs (c)(6)(i) and (ii) of this section,
the replacement cost for a netting set subject to multiple variation
margin agreements or a hybrid netting set must be calculated according
to paragraph (c)(11)(i) of this section.
(7) Potential future exposure of a netting set. The potential future
exposure of a netting set is the product of the PFE multiplier and
the aggregated amount.
(i) PFE multiplier. The PFE multiplier is calculated according to the following formula:
Figure 3. DISPLAY EQUATION
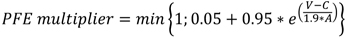
$$
\textit{PFE multiplier}=min \Bigg\{ 1;0.05+0.95\ast e^{ \Big( \frac{V-C}{1.9\ast A} \Big) } \Bigg\}
$$
Where:
V is the sum
of the fair values (after excluding any valuation adjustments) of
the derivative contracts within the netting set;
C is the sum of the net independent
collateral amount and the variation margin amount applicable to the
derivative contracts within the netting set; and
A is the aggregated amount of
the netting set.
(ii) Aggregated amount. The aggregated
amount is the sum of all hedging set amounts, as calculated under
paragraph (c)(8) of this section, within a netting set.
(iii) Multiple
netting sets subject to a single variation margin agreement. Notwithstanding
paragraphs (c)(7)(i) and (ii) of this section and when calculating
the potential future exposure for purposes of total leverage exposure
under section 217.10(c)(2)(ii)(B), the potential future exposure for
multiple netting sets subject to a single variation margin agreement
must be calculated according to paragraph (c)(10)(ii) of this section.
(iv) Netting set subject to multiple variation margin agreements or a
hybrid netting set. Notwithstanding paragraphs (c)(7)(i) and
(ii) of this section and when calculating the potential future exposure
for purposes of total leverage exposure under section 217.10(c)(2)(ii)(B),
the potential future exposure for a netting set subject to multiple
variation margin agreements or a hybrid netting set must be calculated
according to paragraph (c)(11)(ii) of this section.
(8) Hedging set amount.
(i) Interest
rate derivative contracts. To calculate the hedging set amount
of an interest rate derivative contract hedging set, a Board-regulated
institution may use either of the formulas provided in paragraphs
(c)(8)(i)(A) and (B) of this section:
(A) Formula 1 is as follows:
Figure 4. FIGURE 4 DISPLAY
EQUATION
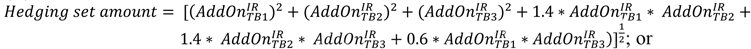
$$
\textit{Hedging set amount}= \Bigg[ \Bigg( AddOn_{TB1}^{IR} \Bigg) ^{2}+ \Bigg( AddOn_{TB2}^{IR} \Bigg) ^{2}+ \Bigg( AddOn_{TB3}^{IR} \Bigg) ^{2}+1.4\ast AddOn_{TB1}^{IR}\ast AddOn_{TB2}^{IR}+1.4\ast AddOn_{TB2}^{IR}\ast AddOn_{TB3}^{IR}+0.6\ast AddOn_{TB1}^{IR}\ast AddOn_{TB3}^{IR} \Bigg) \Bigg] ^{\frac{1}{2}} \text{; or}
$$
(B) Formula 2 is as follows:
Figure 5. FIGURE 5 DISPLAY
EQUATION
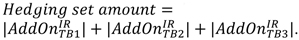
$$
\textit{Hedging set amount}= \vert AddOn_{TB1}^{IR} \vert + \vert AddOn_{TB2}^{IR} \vert + \vert AddOn_{TB3}^{IR} \vert
$$
Where in paragraphs
(c)(8)(i)(A) and (B) of this section:
Figure 6. FIGURE 5 DISPLAY
EQUATION
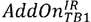
$$
AddOn_{TB1}^{IR}
$$
is the sum of the adjusted derivative contract amounts, as calculated
under paragraph
(c)(9) of this section, within the hedging set with
an end date of less than one year from the present date;
Figure 7. DISPLAY EQUATION
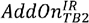
$$
AddOn_{TB2}^{IR}
$$
is the sum of the adjusted derivative contract amounts, as calculated
under paragraph
(c)(9) of this section, within the hedging set with
an end date of one to five years from the present date; and
Figure 8. DISPLAY EQUATION
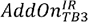
$$
AddOn_{TB3}^{IR}
$$
is the sum of the adjusted derivative contract amounts, as
calculated under paragraph
(c)(9) of this section, within the hedging
set with an end date of more than five years from the present date.
(ii) Exchange rate derivative contracts. For
an exchange rate derivative contract hedging set, the hedging set
amount equals the absolute value of the sum of the adjusted derivative
contract amounts, as calculated under paragraph (c)(9) of this section,
within the hedging set.
(iii) Credit
derivative contracts and equity derivative contracts. The hedging
set amount of a credit derivative contract hedging set or equity derivative
contract hedging set within a netting set is calculated according
to the following formula:
Figure 9. DISPLAY EQUATION
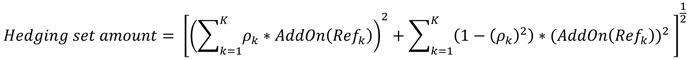
$$
\textit{Hedging set amount}= \Bigg[ \Bigg( \sum\nolimits_{k=1}^{K} \rho _{k}\ast AddOn \Bigg( Ref_{k} \Bigg) \Bigg) ^{2}+ \sum\nolimits _{k=1}^{K} \Bigg( 1- \Bigg( \rho _{k} \Bigg) ^{2} \Bigg) \ast \Bigg( AddOn \Bigg( Ref_{k} \Bigg) \Bigg) ^{2}~ \Bigg] ^{\frac{1}{2}}
$$
Where:
k is each reference
entity within the hedging set.
K is the number of reference
entities within the hedging set.
AddOn (Refk) equals the sum of the adjusted derivative contract amounts,
as determined under paragraph (c)(9) of this section, for all derivative
contracts within the hedging set that reference reference entity k.
ρk equals the applicable supervisory correlation
factor, as provided in Table 3 to this section.
(iv) Commodity
derivative contracts. The hedging set amount of a commodity derivative
contract hedging set within a netting set is calculated according
to the following formula:
Figure 10. FIGURE 10 DISPLAY
EQUATION
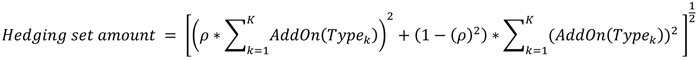
$$
\textit{Hedging set amount} = \Bigg[ \Bigg( \rho \ast \sum\nolimits _{k=1}^{K}AddOn \Bigg( Type_{k} \Bigg) \Bigg) ^{2}+ \Bigg( 1- \Bigg( \rho \Bigg) ^{2} \Bigg) \ast \sum\nolimits _{k=1}^{K} \Bigg( AddOn \Bigg( Type_{k} \Bigg) \Bigg) ^{2}~ \Bigg] ^{\frac{1}{2}}
$$
Where:
k is each commodity
type within the hedging set.
K is the number of commodity
types within the hedging set.
AddOn (Typek) equals the sum of the adjusted derivative contract amounts, as
determined under paragraph (c)(9) of this section, for all derivative
contracts within the hedging set that reference reference commodity
type.
ρ equals
the applicable supervisory correlation factor, as provided in Table
3 to this section.
(v) Basis
derivative contracts and volatility derivative contracts. Notwithstanding
paragraphs (c)(8)(i) through (iv) of this section, a Board-regulated
institution must calculate a separate hedging set amount for each
basis derivative contract hedging set and each volatility derivative
contract hedging set. A Board-regulated institution must calculate
such hedging set amounts using one of the formulas under paragraphs
(c)(8)(i) through (iv) that corresponds to the primary risk factor
of the hedging set being calculated.
(9) Adjusted
derivative contract amount.
(i) Summary. To calculate the adjusted derivative contract amount
of a derivative contract, a Board-regulated institution must determine
the adjusted notional amount of derivative contract, pursuant to paragraph
(c)(9)(ii) of this section, and multiply the adjusted notional amount
by each of the supervisory delta adjustment, pursuant to paragraph
(c)(9)(iii) of this section, the maturity factor, pursuant to paragraph
(c)(9)(iv) of this section, and the applicable supervisory factor,
as provided in Table 3 to this section.
(ii) Adjusted
notional amount.
(A)(1) For an interest rate
derivative contract or a credit derivative contract, the adjusted
notional amount equals the product of the notional amount of the derivative
contract, as measured in U.S. dollars using the exchange rate on the
date of the calculation, and the supervisory duration, as calculated
by the following formula:
Figure 11. FIGURE 10 DISPLAY
EQUATION
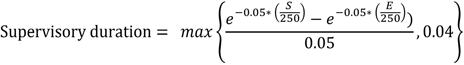
$$
\text{Supervisory duration}=~ max \Bigg\{ \frac{e^{-0.05\ast \Big( \frac{S_{~}}{250} \Big) }-e^{-0.05\ast \Big( \frac{E_{~}}{250} \Big) } \Big) }{0.05},0.04 \Bigg\}
$$
Where:
S is the number of business
days from the present day until the start date of the derivative contract,
or zero if the start date has already passed; and
E is the number of business days from
the present day until the end date of the derivative contract.
(2) For purposes
of paragraph (c)(9)(ii)(A)(1) of this section:
(i) For an interest rate derivative
contract or credit derivative contract that is a variable notional
swap, the notional amount is equal to the time-weighted average of
the contractual notional amounts of such a swap over the remaining
life of the swap; and
(ii) For an interest rate derivative contract or a credit
derivative contract that is a leveraged swap, in which the notional
amount of all legs of the derivative contract are divided by a factor
and all rates of the derivative contract are multiplied by the same
factor, the notional amount is equal to the notional amount of an
equivalent unleveraged swap.
(B)(1) For an exchange rate
derivative contract, the adjusted notional amount is the notional
amount of the non-U.S. denominated currency leg of the derivative
contract, as measured in U.S. dollars using the exchange rate on the
date of the calculation. If both legs of the exchange rate derivative
contract are denominated in currencies other than U.S. dollars, the
adjusted notional amount of the derivative contract is the largest
leg of the derivative contract, as measured in U.S. dollars using
the exchange rate on the date of the calculation.
(2) Notwithstanding paragraph (c)(9)(ii)(B)(1) of this section, for an exchange rate derivative contract
with multiple exchanges of principal, the Board-regulated institution
must set the adjusted notional amount of the derivative contract equal
to the notional amount of the derivative contract multiplied by the
number of exchanges of principal under the derivative contract.
(C)(1)
For an equity derivative contract or a commodity derivative contract,
the adjusted notional amount is the product of the fair value of one unit
of the reference instrument underlying the derivative contract and
the number of such units referenced by the derivative contract.
(2) Notwithstanding
paragraph (c)(9)(ii)(C)(1) of this section, when calculating
the adjusted notional amount for an equity derivative contract or
a commodity derivative contract that is a volatility derivative contract,
the Board-regulated institution must replace the unit price with the
underlying volatility referenced by the volatility derivative contract
and replace the number of units with the notional amount of the volatility
derivative contract.
(iii) Supervisory
delta adjustments.
(A) For a derivative contract that is not
an option contract or collateralized debt obligation tranche, the
supervisory delta adjustment is 1 if the fair value of the derivative
contract increases when the value of the primary risk factor increases
and - 1 if the fair value of the derivative contract decreases when
the value of the primary risk factor increases.
(B) (1) For a derivative
contract that is an option contract, the supervisory delta adjustment
is determined by the following formulas, as applicable:
(1) (i) With prior
written approval from the Board, a Board-regulated institution may
use the internal models methodology in this paragraph (d) to determine
EAD for counterparty credit risk for derivative contracts (collateralized
or uncollateralized) and single-product netting sets thereof, for
eligible margin loans and single-product netting sets thereof, and
for repo-style transactions and single-product netting sets thereof.
(ii) A Board-regulated
institution that uses the internal models methodology for a particular
transaction type (derivative contracts, eligible margin loans, or
repo- style transactions) must use the internal models methodology
for all transactions of that transaction type. A Board-regulated institution
may choose to use the internal models methodology for one or two of
these three types of exposures and not the other types.
(iii) A Board-regulated
institution may also use the internal models methodology for derivative
contracts, eligible margin loans, and repo-style transactions subject
to a qualifying cross-product netting agreement if:
(A) The Board-regulated
institution effectively integrates the risk mitigating effects of
cross-product netting into its risk management and other information
technology systems; and
(B) The Board-regulated institution obtains the prior written approval
of the Board.
(iv) A Board-regulated institution that
uses the internal models methodology for a transaction type must receive
approval from the Board to cease using the methodology for that transaction
type or to make a material change to its internal model.
(2) Risk-weighted assets using IMM. Under the IMM, a Board-regulated
institution uses an internal model to estimate the expected exposure
(EE) for a netting set and then calculates EAD based on that EE. A
Board-regulated institution must calculate two EEs and two EADs (one
stressed and one unstressed) for each netting set as follows:
(i) EADunstressed is calculated using an EE estimate based on the
most recent data meeting the requirements of paragraph (d)(3)(vii)
of this section;
(ii) EADstressed is calculated using an EE estimate based
on a historical period that includes a period of stress to the credit
default spreads of the Board-regulated institution’s counterparties
according to paragraph (d)(3)(viii) of this section;
(iii) The Board-regulated institution
must use its internal model’s probability distribution for changes
in the fair value of a netting set that are attributable to changes
in market variables to determine EE; and
(iv) Under the internal models methodology,
EAD = Max (0, α × effective EPE − CVA), or, subject to the prior
written approval of Board as provided in paragraph (d)(10) of this
section, a more conservative measure of EAD.
(A) CVA equals
the credit valuation adjustment that the Board-regulated institution
has recognized in its balance sheet valuation of any OTC derivative
contracts in the netting set. For purposes of this paragraph (d),
CVA does not include any adjustments to common equity tier 1 capital
attributable to changes in the fair value of the Board-regulated institution’s
liabilities that are due to changes in its own credit risk since the
inception of the transaction with the counterparty.
(B)
Figure 17. DISPLAY EQUATION

$$
\mathit{Effective} \: EPE_{t_k} = \sum^n_{k=1}
$$
Figure 18. DISPLAY EQUATION
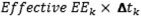
$$
\mathit{Effective} \: EE_k \times \; \Delta t_k
$$
(that
is, effective EPE is the time-weighted average of effective EE where
the weights are the proportion that an individual effective EE represents
in a one-year time interval) where:
(1)
Figure 19. DISPLAY EQUATION
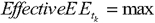
$$
\mathit{Effective}EE_{t_k} = \text{max}
$$
Figure 20. DISPLAY EQUATION
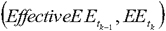
$$
\bigg( \mathit{Effective} EE_{t_{k-1}}, EE_{t_k } \bigg)
$$
(that is, for a specific
date tk, effective EE is the greater of EE at that date
or the effective EE at the previous date); and
(2) tk represents the kth future time period in the model and there are n time periods
represented in the model over the first year, and
(C) α = 1.4 except as provided
in paragraph (d)(6) of this section, or when the Board has determined
that the Board-regulated institution must set α higher based on the
Board-regulated institution’s specific characteristics of counterparty
credit risk or model performance.
(v) A Board-regulated institution may
include financial collateral currently posted by the counterparty
as collateral (but may not include other forms of collateral) when
calculating EE.
(vi) If a Board-regulated institution hedges some or all of the counterparty
credit risk associated with a netting set using an eligible credit
derivative, the Board-regulated institution may take the reduction
in exposure to the counterparty into account when estimating EE. If
the Board-regulated institution recognizes this reduction in exposure
to the counterparty in its estimate of EE, it must also use its internal
model to estimate a separate EAD for the Board-regulated institution’s
exposure to the protection provider of the credit derivative.
(3) Prior approval relating to EAD calculation. To obtain Board approval to calculate the distributions of exposures
upon which the EAD calculation is based, the Board-regulated institution
must demonstrate to the satisfaction of the Board that it has been
using for at least one year an internal model that broadly meets the
following minimum standards, with which the Board-regulated institution
must maintain compliance:
(i) The model must have the systems
capability to estimate the expected exposure to the counterparty on
a daily basis (but is not expected to estimate or report expected
exposure on a daily basis);
(ii) The model must estimate expected
exposure at enough future dates to reflect accurately all the future
cash flows of contracts in the netting set;
(iii) The model must account for the
possible non-normality of the exposure distribution, where appropriate;
(iv) The Board-regulated
institution must measure, monitor, and control current counterparty
exposure and the exposure to the counterparty over the whole life
of all contracts in the netting set;
(v) The Board-regulated institution
must be able to measure and manage current exposures gross and net
of collateral held, where appropriate. The Board-regulated institution
must estimate expected exposures for OTC derivative contracts both
with and without the effect of collateral agreements;
(vi) The Board-regulated institution
must have procedures to identify, monitor, and control wrong-way risk
throughout the life of an exposure. The procedures must include stress
testing and scenario analysis;
(vii) The model must use current market
data to compute current exposures. The Board-regulated institution
must estimate model parameters using historical data from the most
recent three-year period and update the data quarterly or more frequently
if market conditions warrant. The Board-regulated institution should consider
using model parameters based on forward-looking measures, where appropriate;
(viii) When estimating
model parameters based on a stress period, the Board-regulated institution
must use at least three years of historical data that include a period
of stress to the credit default spreads of the Board-regulated institution’s
counterparties. The Board-regulated institution must review the data
set and update the data as necessary, particularly for any material
changes in its counterparties. The Board-regulated institution must
demonstrate, at least quarterly, and maintain documentation of such
demonstration, that the stress period coincides with increased CDS
or other credit spreads of the Board-regulated institution’s counterparties.
The Board-regulated institution must have procedures to evaluate the
effectiveness of its stress calibration that include a process for
using benchmark portfolios that are vulnerable to the same risk factors
as the Board-regulated institution’s portfolio. The Board may require
the Board-regulated institution to modify its stress calibration to
better reflect actual historic losses of the portfolio;
(ix) A Board-regulated
institution must subject its internal model to an initial validation
and annual model review process. The model review should consider
whether the inputs and risk factors, as well as the model outputs,
are appropriate. As part of the model review process, the Board-regulated
institution must have a backtesting program for its model that includes
a process by which unacceptable model performance will be determined
and remedied;
(x)
A Board-regulated institution must have policies for the measurement,
management and control of collateral and margin amounts; and
(xi) A Board-regulated institution
must have a comprehensive stress testing program that captures all
credit exposures to counterparties, and incorporates stress testing
of principal market risk factors and creditworthiness of counterparties.
(4) Calculating the maturity of exposures.
(i) If the remaining maturity of the exposure or the longest-dated
contract in the netting set is greater than one year, the Board-regulated
institution must set M for the exposure or netting set equal to the
lower of five years or M(EPE), where:
(A)
Figure 21. DISPLAY EQUATION
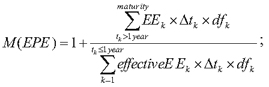
$$
M(EPE)=1 + \frac{
{\sum\limits^{\mathit{maturity}}_{t_k > \text{1 year}}} EE_k \times \Delta t_k \times df_k
}
{
{\sum\limits^{t_k \leq \text{1 year}}_{k=1} }
effectiveE \: E_k \times \Delta t_k \times df_k} \text{ ;}
$$
(B) dfk is the
risk-free discount factor for future time period tk; and
(C) Δt k = t k − t kâ1.
(ii) If the remaining maturity of the
exposure or the longest-dated contract in the netting set is one year
or less, the Board-regulated institution must set M for the exposure
or netting set equal to one year, except as provided in section 217.131(d)(7).
(iii) Alternatively,
a Board-regulated institution that uses an internal model to calculate
a one-sided credit valuation adjustment may use the effective credit
duration estimated by the model as M(EPE) in place of the formula
in paragraph (d)(4)(i) of this section.
(5) Effects of
collateral agreements on EAD. A Board-regulated institution may
capture the effect on EAD of a collateral agreement that requires
receipt of collateral when exposure to the counterparty increases,
but may not capture the effect on EAD of a collateral agreement that
requires receipt of collateral when counterparty credit quality deteriorates.
Two methods are available to capture the effect of a collateral agreement,
as set forth in paragraphs (d)(5)(i) and (ii) of this section:
(i) With prior written approval from the Board, a Board-regulated
institution may include the effect of a collateral agreement within
its internal model used to calculate EAD. The Board-regulated institution
may set EAD equal to the expected exposure at the end
of the margin period of risk. The margin period of risk means, with
respect to a netting set subject to a collateral agreement, the time
period from the most recent exchange of collateral with a counterparty
until the next required exchange of collateral, plus the period of
time required to sell and realize the proceeds of the least liquid
collateral that can be delivered under the terms of the collateral
agreement and, where applicable, the period of time required to re-hedge
the resulting market risk upon the default of the counterparty. The
minimum margin period of risk is set according to paragraph (d)(5)(iii)
of this section; or
(ii) As an alternative to paragraph (d)(5)(i) of this section, a
Board-regulated institution that can model EPE without collateral
agreements but cannot achieve the higher level of modeling sophistication
to model EPE with collateral agreements can set effective EPE for
a collateralized netting set equal to the lesser of:
(A) An add-on
that reflects the potential increase in exposure of the netting set
over the margin period of risk, plus the larger of:
(1) The current exposure of the netting
set reflecting all collateral held or posted by the Board-regulated
institution excluding any collateral called or in dispute; or
(2) The largest net exposure
including all collateral held or posted under the margin agreement
that would not trigger a collateral call. For purposes of this section,
the add-on is computed as the expected increase in the netting set’s
exposure over the margin period of risk (set in accordance with paragraph
(d)(5)(iii) of this section); or
(B) Effective EPE without a collateral agreement
plus any collateral the Board-regulated institution posts to the counterparty
that exceeds the required margin amount.
(iii) For purposes of this
part, including paragraphs (d)(5)(i) and (ii) of this section, the
margin period of risk for a netting set subject to a collateral agreement
is:
(A) Five business days for repo-style transactions subject to daily
remargining and daily marking-to-market, and ten business days for
other transactions when liquid financial collateral is posted under
a daily margin maintenance requirement, or
(B) Twenty business days if the number of
trades in a netting set exceeds 5,000 at any time during the previous
quarter (except if the Board-regulated institution is calculating
EAD for a cleared transaction under section 217.133) or contains one
or more trades involving illiquid collateral or any derivative contract
that cannot be easily replaced. If over the two previous quarters
more than two margin disputes on a netting set have occurred that
lasted more than the margin period of risk, then the Board-regulated
institution must use a margin period of risk for that netting set
that is at least two times the minimum margin period of risk for that
netting set. If the periodicity of the receipt of collateral is N-days,
the minimum margin period of risk is the minimum margin period of
risk under this paragraph (d) plus N minus 1. This period should be
extended to cover any impediments to prompt re-hedging of any market
risk.
(C) Five business
days for an OTC derivative contract or netting set of OTC derivative
contracts where the Board-regulated institution is either acting as
a financial intermediary and enters into an offsetting transaction
with a CCP or where the Board-regulated institution provides a guarantee
to the CCP on the performance of the client. A Board-regulated institution
must use a longer holding period if the Board-regulated institution
determines that a longer period is appropriate. Additionally, the
Board may require the Board-regulated institution to set a longer
holding period if the Board determines that a longer
period is appropriate due to the nature, structure, or characteristics
of the transaction or is commensurate with the risks associated with
the transaction.
(6) Own estimate
of alpha. With prior written approval of the Board, a Board-regulated
institution may calculate alpha as the ratio of economic capital from
a full simulation of counterparty exposure across counterparties that
incorporates a joint simulation of market and credit risk factors
(numerator) and economic capital based on EPE (denominator), subject
to a floor of 1.2. For purposes of this calculation, economic capital
is the unexpected losses for all counterparty credit risks measured
at a 99.9 percent confidence level over a one-year horizon. To receive
approval, the Board-regulated institution must meet the following
minimum standards to the satisfaction of the Board:
(i) The
Board-regulated institution’s own estimate of alpha must capture in
the numerator the effects of:
(A) The material sources of stochastic
dependency of distributions of fair values of transactions or portfolios
of transactions across counterparties;
(B) Volatilities and correlations of market
risk factors used in the joint simulation, which must be related to
the credit risk factor used in the simulation to reflect potential
increases in volatility or correlation in an economic downturn, where
appropriate; and
(C) The
granularity of exposures (that is, the effect of a concentration in
the proportion of each counterparty’s exposure that is driven by a
particular risk factor).
(ii) The Board-regulated institution
must assess the potential model uncertainty in its estimates of alpha.
(iii) The Board-regulated
institution must calculate the numerator and denominator of alpha
in a consistent fashion with respect to modeling methodology, parameter
specifications, and portfolio composition.
(iv) The Board-regulated institution
must review and adjust as appropriate its estimates of the numerator
and denominator of alpha on at least a quarterly basis and more frequently
when the composition of the portfolio varies over time.
(7) Risk-based capital requirements for transactions with specific wrong-way
risk. A Board-regulated institution must determine if a repo-style
transaction, eligible margin loan, bond option, or equity derivative
contract or purchased credit derivative to which the Board-regulated
institution applies the internal models methodology under this paragraph
(d) has specific wrong-way risk. If a transaction has specific wrong-way
risk, the Board-regulated institution must treat the transaction as
its own netting set and exclude it from the model described in section
217.132(d)(2) and instead calculate the risk-based capital requirement
for the transaction as follows:
(i) For an equity derivative
contract, by multiplying:
(A) K, calculated using the appropriate risk-based
capital formula specified in Table 1 of section 217.131 using the
PD of the counterparty and LGD equal to 100 percent, by
(B) The maximum amount the Board-regulated
institution could lose on the equity derivative.
(ii) For a purchased
credit derivative by multiplying:
(A) K, calculated using the appropriate
risk-based capital formula specified in Table 1 of section 217.131
using the PD of the counterparty and LGD equal to 100 percent, by
(B) The fair value of the
reference asset of the credit derivative.
(iii) For a bond option,
by multiplying:
(A) K, calculated using the appropriate risk-based
capital formula specified in Table 1 of section 217.131 using the
PD of the counterparty and LGD equal to 100 percent, by
(B) The smaller of the notional
amount of the underlying reference asset and the maximum potential
loss under the bond option contract.
(iv) For a repo-style transaction
or eligible margin loan by multiplying:
(A) K, calculated using the
appropriate risk-based capital formula specified in Table 1 of section
217.131 using the PD of the counterparty and LGD equal to 100 percent,
by
(B) The EAD of the
transaction determined according to the EAD equation in section 217.132(b)(2),
substituting the estimated value of the collateral assuming a default
of the counterparty for the value of the collateral in ΣC of
the equation.
(8) Risk-weighted
asset amount for IMM exposures with specific wrong-way risk. The
aggregate risk-weighted asset amount for IMM exposures with specific
wrong-way risk is the sum of a Board-regulated institution’s risk-based
capital requirement for purchased credit derivatives that are not
bond options with specific wrong-way risk as calculated under paragraph
(d)(7)(ii) of this section, a Board-regulated institution’s risk-based
capital requirement for equity derivatives with specific wrong-way
risk as calculated under paragraph (d)(7)(i) of this section, a Board-regulated
institution’s risk-based capital requirement for bond options with
specific wrong-way risk as calculated under paragraph (d)(7)(iii)
of this section, and a Board-regulated institution’s risk-based capital
requirement for repo-style transactions and eligible margin loans
with specific wrong-way risk as calculated under paragraph (d)(7)(iv)
of this section, multiplied by 12.5.
(9) Risk-weighted
assets for IMM exposures.
(i) The Board-regulated
institution must insert the assigned risk parameters for each counterparty
and netting set into the appropriate formula specified in Table 1
of section 217.131 and multiply the output of the formula by the EADunstressed of the netting set to obtain the unstressed capital
requirement for each netting set. A Board-regulated institution that
uses an advanced CVA approach that captures migrations in credit spreads
under paragraph (e)(3) of this section must set the maturity adjustment
(b) in the formula equal to zero. The sum of the unstressed capital
requirement calculated for each netting set equals Kunstressed.
(ii) The Board-regulated
institution must insert the assigned risk parameters for each wholesale
obligor and netting set into the appropriate formula specified in
Table 1 of section 217.131 and multiply the output of the formula
by the EADstressed of the netting set to obtain the stressed
capital requirement for each netting set. A Board-regulated institution
that uses an advanced CVA approach that captures migrations in credit
spreads under paragraph (e)(6) of this section must set the maturity
adjustment (b) in the formula equal to zero. The sum of the stressed
capital requirement calculated for each netting set equals Kstressed.
(iii) The Board-regulated
institution’s dollar risk-based capital requirement under the internal
models methodology equals the larger of Kunstressed and
Kstressed. A Board-regulated institution’s risk-weighted
assets amount for IMM exposures is equal to the capital requirement
multiplied by 12.5, plus risk-weighted assets for IMM exposures with
specific wrong-way risk in paragraph (d)(8) of this section and those
in paragraph (d)(10) of this section.
(10) Other measures
of counterparty exposure.
(i) With prior written
approval of the Board, a Board-regulated institution may set EAD equal
to a measure of counterparty credit risk exposure, such as peak EAD,
that is more conservative than an alpha of 1.4 times the larger of
EPEunstressed and EPEstressed for every counterparty
whose EAD will be measured under the alternative measure of counterparty
exposure. The Board-regulated institution must demonstrate the conservatism
of the measure of counterparty credit risk exposure used for EAD.
With respect to paragraph (d)(10)(i) of this section:
(A) For material
portfolios of new OTC derivative products, the Board-regulated institution
may assume that the standardized approach for counterparty credit
risk pursuant to paragraph (c) of this section meets the conservatism
requirement of this section for a period not to exceed 180 days.
(B) For immaterial portfolios
of OTC derivative contracts, the Board-regulated institution generally
may assume that the standardized approach for counterparty credit
risk pursuant to paragraph (c) of this section meets the conservatism
requirement of this section.
(ii) To calculate risk-weighted assets
for purposes of the approach in paragraph (d)(10)(i) of this section,
the Board-regulated institution must insert the assigned risk parameters
for each counterparty and netting set into the appropriate formula
specified in Table 1 of section 217.131, multiply the output of the
formula by the EAD for the exposure as specified above, and multiply
by 12.5.
(1) In general. With respect to its OTC derivative contracts, a Board-regulated
institution must calculate a CVA risk-weighted asset amount for its
portfolio of OTC derivative transactions that are subject to the CVA
capital requirement using the simple CVA approach described in paragraph
(e)(5) of this section or, with prior written approval of the Board,
the advanced CVA approach described in paragraph (e)(6) of this section.
A Board-regulated institution that receives prior Board approval to
calculate its CVA risk-weighted asset amounts for a class of counterparties
using the advanced CVA approach must continue to use that approach
for that class of counterparties until it notifies the Board in writing
that the Board-regulated institution expects to begin calculating
its CVA risk-weighted asset amount using the simple CVA approach.
Such notice must include an explanation of the Board-regulated institution’s
rationale and the date upon which the Board-regulated institution
will begin to calculate its CVA risk-weighted asset amount using the
simple CVA approach.
(2) Market risk Board-regulated institutions. Notwithstanding the prior approval requirement in paragraph (e)(1)
of this section, a market risk Board-regulated institution may calculate
its CVA risk-weighted asset amount using the advanced CVA approach
if the Board-regulated institution has Board approval to:
(i) Determine
EAD for OTC derivative contracts using the internal models methodology
described in paragraph (d) of this section; and
(ii) Determine its specific risk add-on
for debt positions issued by the counterparty using a specific risk
model described in section 217.207(b).
(3) Recognition
of hedges.
(i) A Board-regulated institution may
recognize a single name CDS, single name contingent CDS, any other
equivalent hedging instrument that references the counterparty directly,
and index credit default swaps (CDSind) as a CVA hedge
under paragraph (e)(5)(ii) of this section or paragraph (e)(6) of
this section, provided that the position is managed as a CVA hedge
in accordance with the Board-regulated institution’s hedging policies.
(ii) A Board-regulated
institution shall not recognize as a CVA hedge any tranched or nth-to-default credit derivative.
(4) Total CVA
risk-weighted assets. Total CVA risk-weighted assets is the CVA
capital requirement, KCVA, calculated for a Board-regulated
institution’s entire portfolio of OTC derivative counterparties that
are subject to the CVA capital requirement, multiplied by 12.5.
(5) Simple CVA approach.
(i) Under
the simple CVA approach, the CVA capital requirement, KCVA, is calculated according to the following formula:
Figure 22. DISPLAY EQUATION
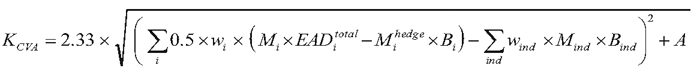
$$
K_{CVA} = 2.33 \times \sqrt{
\Bigg \lgroup
{\sum\limits_i}0.5 \times w_i \times \bigg(M_i \times EAD^{\mathit{total}}_i - M^{\mathit{hedge}}_i \times B_i \bigg) -
{\sum\limits_{ind}} w_{ind} \times M_{ind} \times B_{ind}
\Bigg \rgroup ^2 + A
}
$$
Where:
Figure 23. DISPLAY EQUATION
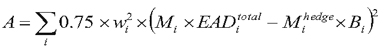
$$
A = {\sum\limits_i} 0.75 \times w^2_i \times \big( M_i \times EAD^{\mathit{total}}_i - M^{\mathit{headge}}_i \times B_i \big)^2
$$
(A) wi = the weight applicable
to counterparty i under Table 4 to this section;
(B) Mi = the EAD-weighted average
of the effective maturity of each netting set with counterparty i (where each netting set’s effective maturity can be no less
than one year.)
(C) EADitotal = the sum of the EAD for all netting sets
of OTC derivative contracts with counterparty i calculated
using the standardized approach to counterparty credit risk described
in paragraph (c) of this section or the internal models methodology
described in paragraph (d) of this section. When the Board-regulated
institution calculates EAD under paragraph (c) of this section, such
EAD may be adjusted for purposes of calculating EADitotal by multiplying EAD by (1-exp(-0.05 × Mi))/(0.05
× Mi), where “exp” is the exponential function. When the
Board-regulated institution calculates EAD under paragraph (d) of
this section, EADitotal equals EADunstressed.
(D) Mihedge = the notional weighted average maturity of the hedge
instrument.
(E) Bi = the sum of the notional amounts of any purchased single
name CDS referencing counterparty i that is used to hedge CVA
risk to counterparty i multiplied by (1-exp(-0.05 × Mihedge))/(0.05 × Mihedge).
(F) Mind = the maturity
of the CDSind or the notional weighted average maturity
of any CDSind purchased to hedge CVA risk of counterparty i.
(G) Bind = the notional amount of one or more CDSind purchased
to hedge CVA risk for counterparty i multiplied by (1-exp(-0.05
× M ind))/(0.05 × M ind)
(H) w ind = the weight applicable to the CDSind based on the average weight of the underlying reference names that
comprise the index under Table 4 to this section.
(ii) The Board-regulated
institution may treat the notional amount of the index attributable
to a counterparty as a single name hedge of counterparty i (B i,) when calculating KCVA, and
subtract the notional amount of B i from
the notional amount of the CDSind. A Board-regulated institution
must treat the CDSind hedge with the notional amount reduced
by B i as a CVA hedge.
Table 4 to section
217.132—Assignment of counterparty weight
| Internal PD (in percent) |
Weight wi (in percent) |
| 0.00-0.07 |
0.70 |
| >0.070-0.15 |
0.80 |
| >0.15-0.40 |
1.00 |
| >0.40-2.00 |
2.00 |
| >2.00-6.00 |
3.00 |
| >6.00 |
10.00 |
(6) Advanced CVA approach.
(i) A Board-regulated
institution may use the VaR model that it uses to determine specific
risk under section 217.207(b) or another VaR model that meets the
quantitative requirements of section 217.205(b) and section 217.207(b)(1)
to calculate its CVA capital requirement for a counterparty by modeling
the impact of changes in the counterparties’ credit spreads, together
with any recognized CVA hedges, on the CVA for the counterparties,
subject to the following requirements:
(A) The VaR model must incorporate only changes
in the counterparties’ credit spreads, not changes in other risk factors.
The VaR model does not need to capture jump-to-default risk;
(B) A Board-regulated institution
that qualifies to use the advanced CVA approach must include in that
approach any immaterial OTC derivative portfolios for which it uses
the standardized approach to counterparty credit risk in paragraph
(c) of this section according to paragraph (e)(6)(viii) of this section;
and
(C) A Board-regulated
institution must have the systems capability to calculate the CVA
capital requirement for a counterparty on a daily basis (but is not
required to calculate the CVA capital requirement on a daily basis).
(ii)
Under the advanced CVA approach, the CVA capital requirement, KCVA, is calculated according to the following formulas:
Figure 24. DISPLAY EQUATION
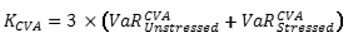
$$
K_{CVA} = 3 \times \bigg( VaR^{\mathit{CVA}}_{\mathit{Unstressed}} + VaR^{\mathit{CVA}}_{\mathit{Stressed}} \bigg)
$$
where VaR CVAj is the 99% VaR reflecting
changes of CVA j and fair value of eligible
hedges (aggregated across all counterparties and eligible hedges)
resulting from simulated changes of credit spreads over a 10-day time
horizon. CVA j for a given counterparty must
be calculated according to
Figure 25. DISPLAY EQUATION
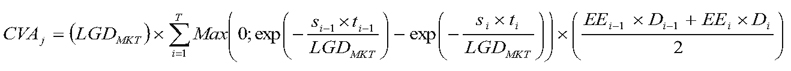
$$
CVA_j =
\bigg( LGD_{MKT} \bigg) \times
{\sum\limits^T_{i=1}} Max
\Bigg \lgroup
0; \text{exp}
\Bigg \lgroup
-
\frac{s_{i-1} \times t_{i-1}}{LGD_{MKT}}
\Bigg \rgroup
- \text{exp}
\Bigg \lgroup
-
\frac{s_i \times t_i}{LGD_{MKT}}
\Bigg \rgroup
\Bigg \rgroup
\times
\Bigg \lgroup
\frac{EE_{i-1} \times D_{i-1} + EE_i \times D_i}{2}
\Bigg \rgroup
$$
Where
(A) t i = the time
of the i -th revaluation time bucket starting from t 0 = 0.
(B) t T = the longest contractual maturity
across the OTC derivative contracts with the counterparty.
(C) s i = the CDS spread for the counterparty at tenor t i used to calculate the CVA for the counterparty. If a
CDS spread is not available, the Board-regulated institution must
use a proxy spread based on the credit quality, industry and region
of the counterparty.
(D) LGD MKT = the loss given default of the counterparty
based on the spread of a publicly traded debt instrument of the counterparty,
or, where a publicly traded debt instrument spread is not available,
a proxy spread based on the credit quality, industry, and region of
the counterparty. Where no market information and no reliable proxy
based on the credit quality, industry, and region of the counterparty
are available to determine LGDMKT, a Board-regulated institution
may use a conservative estimate when determining LGDMKT, subject to approval by the Board.
(E) EE i = the sum
of the expected exposures for all netting sets with the counterparty
at revaluation time t i, calculated according
to paragraphs (e)(6)(iv)(A) and (e)(6)(v)(A) of this section.
(F) D i = the risk-free discount factor at time t i, where D 0 = 1.
(G) Exp is the exponential function.
(H) The subscript j refers either
to a stressed or an unstressed calibration as described in paragraphs
(e)(6)(iv) and (v) of this section.
(iii) Notwithstanding paragraphs (e)(6)(i)
and (e)(6)(ii) of this section, a Board-regulated institution must
use the formulas in paragraphs (e)(6)(iii)(A) or (e)(6)(iii)(B) of
this section to calculate credit spread sensitivities if its VaR model
is not based on full repricing.
(A) If the VaR model is based
on credit spread sensitivities for specific tenors, the Board-regulated
institution must calculate each credit spread sensitivity according
to the following formula:
Regulatory CS01 =
Figure 26. DISPLAY EQUATION
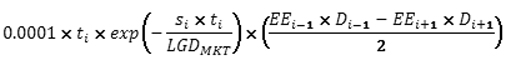
$$
0.0001 \times t_i \times exp
\Bigg(-
\frac{s_i \times t_i}{LGD_{MKT}}
\Bigg)
\times
\bigg(
\frac{EE_{i-1} \times D_{i-1} - EE_{i+1} \times D_{i+1}}{2}
\bigg)
$$
For
the final time bucket i = T, the corresponding formula is
Regulatory CS01 =
Figure 27. DISPLAY EQUATION
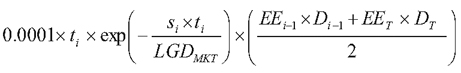
$$
0.0001 \times t_i \times \text{exp}
\Bigg \lgroup -
\frac{s_i \times t_i}{LGD_{MKT}}
\Bigg \rgroup
\times
\Bigg \lgroup
\frac{EE_{i-1} \times D_{i-1} + EE_T \times D_T}{2}
\Bigg \rgroup
$$
(B) If the VaR model uses credit spread sensitivities to parallel
shifts in credit spreads, the Board-regulated institution must calculate
each credit spread sensitivity according to the following formula:
Regulatory CS01 =
Figure 28. DISPLAY EQUATION
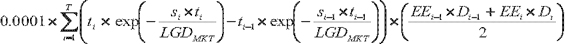
$$
0.0001 \times
{\sum\limits^T_{i=1}}
\Bigg \lgroup
t_i \times \text{exp}
\bigg \lgroup
-
\frac{s_i \times t_i}{LGD_{MKT}}
\bigg \rgroup
- t_{i-1} \times \text{exp}
\bigg \lgroup
-
\frac{s_{i-1} \times t_{i-1}}{LGD_{MKT}}
\bigg \rgroup
\Bigg \rgroup
\times
\Bigg \lgroup
\frac{EE_{i-1} \times D_{i-1} + EE_i \times D_i}{2}
\Bigg \rgroup
$$
(iv) To calculate the CVAUnstressed measure for purposes of paragraph (e)(6)(ii) of this section, the
Board-regulated institution must:
(A) Use the EE i calculated using the calibration of paragraph (d)(3)(vii)
of this section, except as provided in section 217.132 (e)(6)(vi),
and
(B) Use the historical
observation period required under section 217.205(b)(2).
(v) To calculate the CVA Stressed measure for purposes of paragraph
(e)(6)(ii) of this section, the Board-regulated institution must:
(A) Use the EE i calculated using the stress
calibration in paragraph (d)(3)(viii) of this section except as provided
in paragraph (e)(6)(vi) of this section.
(B) Calibrate VaR model inputs to historical
data from the most severe twelve-month stress period contained within
the three-year stress period used to calculate EE i. The Board may require a Board-regulated institution to use
a different period of significant financial stress in the calculation
of the CVA Stressed measure.
(vi) If a Board-regulated
institution captures the effect of a collateral agreement on EAD using
the method described in paragraph (d)(5)(ii) of this section, for
purposes of paragraph (e)(6)(ii) of this section, the Board-regulated
institution must calculate EE i using the
method in paragraph (d)(5)(ii) of this section and keep that EE constant
with the maturity equal to the maximum of:
(A) Half of the longest maturity
of a transaction in the netting set, and
(B) The notional weighted average maturity
of all transactions in the netting set.
(vii) For purposes of paragraph
(e)(6) of this section, the Board-regulated institution’s VaR model
must capture the basis between the spreads of any CDSind that is used as the hedging instrument and the hedged counterparty
exposure over various time periods, including benign and stressed
environments. If the VaR model does not capture that basis, the Board-regulated
institution must reflect only 50 percent of the notional amount of
the CDSind hedge in the VaR model.
(viii) If a Board-regulated institution
uses the standardized approach for counterparty credit risk pursuant
to paragraph (c) of this section to calculate the EAD for any immaterial
portfolios of OTC derivative contracts, the Board-regulated institution
must use that EAD as a constant EE in the formula for the calculation
of CVA with the maturity equal to the maximum of:
(A) Half of the
longest maturity of a transaction in the netting set; and
(B) The notional weighted average
maturity of all transactions in the netting set.