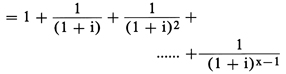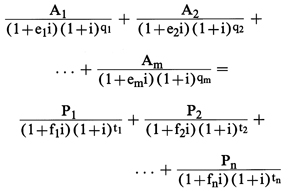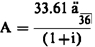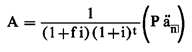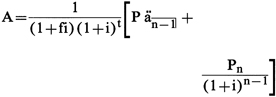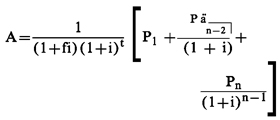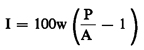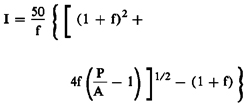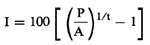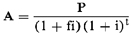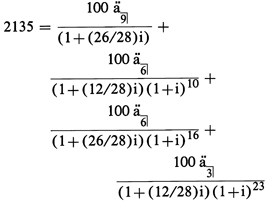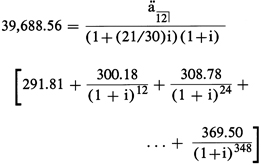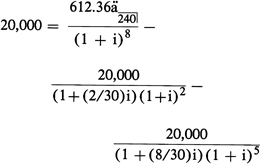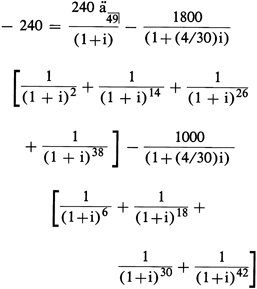(1) General rule. The annual percentage rate shall be the nominal annual percentage
rate determined by multiplying the unit-period rate by the number
of unit periods in a year.
(2) Term of the
transaction. The term of the transaction begins on the date of
its consummation, except that if the finance charge or any portion
of it is earned beginning on a later date, the term begins on the
later date. The term ends on the date the last payment is due, except
that if an advance is scheduled after that date, the term ends on
the later date. For computation purposes, the length of the term shall
be equal to the time interval between any point in time on the beginning
date to the same point in time on the ending date.
(3) Definitions
of time intervals.
(i) A period is the interval of time
between advances or between payments and includes the interval of
time between the date the finance charge begins to be earned and the
date of the first advance thereafter or the date of the first payment
thereafter, as applicable.
(ii) A common period is any period that
occurs more than once in a transaction.
(iii) A standard interval of time is
a day, week, semimonth, month, or a multiple of a week or a month
up to, but not exceeding, one year.
(iv) All months shall be considered
equal. Full months shall be measured from any point in time on a given
date of a given month to the same point in time on the same date of
another month. If a series of payments (or advances) is scheduled
for the last day of each month, months shall be measured from the
last day of the given month to the last day of another month. If payments
(or advances) are scheduled for the 29th or 30th of each month, the
last day of February shall be used when applicable.
(4) Unit period.
(i) In all transactions
other than a single advance, single payment transaction, the unit
period shall be that common period, not to exceed 1 year, that occurs
most frequently in the transaction, except that
(A) If two or
more common periods occur with equal frequency, the smaller of such
common periods shall be the unit period; or
(B) If there is no common period in the transaction,
the unit period shall be that period which is the average of all periods
rounded to the nearest whole standard interval of time. If the average
is equally near two standard intervals of time, the lower shall be
the unit period.
(ii) In a single advance, single payment
transaction, the unit period shall be the term of the transaction,
but shall not exceed one year.
(5) Number of
unit periods between two given dates.
(i) The number of days
between two dates shall be the number of 24-hour intervals between
any point in time on the first date to the same point in time on the
second date.
(ii)
If the unit period is a month, the number of full unit periods between
two dates shall be the number of months measured back from the later
date. The remaining fraction of a unit period shall be the number
of days measured forward from the earlier date to the beginning of
the first full unit period, divided by 30. If the unit period is a
month, there are 12 unit periods per year.
(iii) If the unit period is a semimonth
or a multiple of a month not exceeding 11 months, the number of days
between two dates shall be 30 times the number of full months measured
back from the later date, plus the number of remaining days. The number
of full unit periods and the remaining fraction of a unit period shall
be determined by dividing such number of days by 15 in the case of
a semimonthly unit period or by the appropriate multiple of 30 in
the case of a multimonthly unit period. If the unit period is a semimonth,
the number of unit periods per year shall be 24. If the number of
unit periods is a multiple of a month, the number of unit periods
per year shall be 12 divided by the number of months per unit period.
(iv) If the unit period
is a day, a week, or a multiple of a week, the number of full unit
periods and the remaining fractions of a unit period shall be determined
by dividing the number of days between the two given dates by the
number of days per unit period. If the unit period is a day, the number
of unit periods per year shall be 365. If the unit period is a week
or a multiple of a week, the number of unit periods per year shall
be 52 divided by the number of weeks per unit period.
(v) If the unit period
is a year, the number of full unit periods between two dates shall
be the number of full years (each equal to 12 months) measured back
from the later date. The remaining fraction of a unit period shall
be
(A) The remaining number of months divided
by 12 if the remaining interval is equal to a whole number of months,
or
(B) The remaining number
of days divided by 365 if the remaining interval is not equal to a
whole number of months.
(vi) In a single advance, single payment
transaction in which the term is less than a year and is equal to
a whole number of months, the number of unit periods in the term shall
be one, and the number of unit periods per year shall be 12 divided
by the number of months in the term or 365 divided by the number of
days in the term.
(vii) In a single advance, single payment transaction in which the
term is less than a year and is not equal to a whole number
of months, the number of unit periods in the term shall be one, and
the number of unit periods per year shall be 365 divided by the number
of days in the term.
(6) Percentage
rate for a fraction of a unit period. The percentage rate of
finance charge for a fraction (less than one) of a unit period
shall be equal to such fraction multiplied by the percentage rate
of finance charge per unit period.
(7) Symbols. The symbols used to express the terms of a transaction in the equation
set forth in paragraph (b)(8) of this section are defined as follows:
Symbols
| Ak |
= |
The amount of the kth advance. |
| qk |
= |
The number of full unit periods from the
beginning of the term of the transaction to the kth advance. |
| ek |
= |
The fraction of a unit period in the time
interval from the beginning of the term of the transaction to the
kth advance. |
| m |
= |
The number of advances. |
| Pj |
= |
The amount of the jth payment. |
| tj |
= |
The number of full unit periods from the
beginning of the term of the transaction to the jth payment. |
| fj |
= |
The fraction of a unit period in the time
interval from the beginning of the term of the transaction to the
jth payment. |
| n |
= |
The number of payments. |
| i |
= |
The percentage rate of finance charge per
unit period, expressed as a decimal equivalent. |
Symbols used
in the examples shown in this appendix are defined as follows:
Symbols used
in the examples
<mb;-6q>..<mb;0q><mh;-4.5q>a|m-<mb;4q><mh;-5.5q>x<mb;2q><tmpsz;6q>1<reset>
$$
\require{enclose}
\mathrm{\ddot{a}_{\enclose{actuarial}{x}}} =
$$
|
= |
The present value of 1 per unit period for
x unit periods, first payment due immediately. |
Figure 1. DISPLAY EQUATION
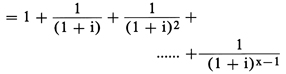
$$\mathrm{=1 + \frac{1}{(1 + i)}} + \frac{1}{(1 + \mathrm{i})^2}+ \\
\qquad\qquad\qquad\qquad\qquad\qquad\qquad....+ \frac{1}{(1 + \mathrm{i})^{\mathrm{x}-1}}
$$
Symbols used
in the examples
| w |
= |
The number of unit periods per year. |
| I |
= |
wi × 100 = The nominal annual percentage
rate. |
(8) General equation. The following equation
sets forth the relationship among the terms of a transaction:
Figure 2. DISPLAY EQUATION
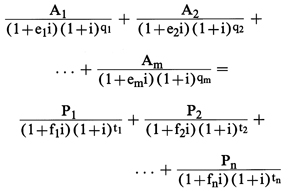
$$
\mathrm{\frac{A_1}{(1+e_1i)(1+i)^{q_1}} + \frac{A_2}{(1+e_2i)(1+i)^{q_2}} +}
\\
\qquad\qquad...+ \mathrm{\frac{A_m}{(1+e_mi)(1+i)^{q_m}}} =
\\
\qquad \mathrm{\frac{P_1}{(1+f_1i)(1+i)^{t_1}} + \frac{P_2}{(1+f_2i)(1+i)^{t_2}} +}
\\
\qquad\qquad\qquad\qquad\qquad...+ \mathrm{\frac{P_n}{(1+f_ni)(1+i)^{t_n}}}
$$
(9) Solution of general equation by iteration process.
(i) The general equation in paragraph
(b)(8) of this section, when applied to a simple transaction in which
a loan of $1000 is repaid by 36 monthly payments of $33.61 each, takes
the special form:
Figure 3. DISPLAY EQUATION
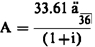
$$
\require{enclose}
\mathrm{A = \frac{33.61\ddot{a}_{\enclose{actuarial}{36}}}{(1+i)}}
$$
Step 1:
- Let I1 = estimated annual percentage rate
=%12.50%
- Evaluate expression for A, letting i = I1 /(100w) = %.010416667
- Results (referred to as A‘) =%1004.674391
Step 2:
- Let I2 = I1 +.1 =%12.60%
- Evaluate expression for A, letting i = I2 /(100w) = %.010500000
- Result (referred to as A“) =%1003.235366
Step 3:
- Interpolate for I (annual percentage rate):
Figure 4. DISPLAY EQUATION

$$
\mathrm{I = I_1 + .1}
\begin{bmatrix}
\mathrm{(A-A^{\prime})} \\[0.3em]
\hline
\mathrm{(A^{\prime\prime}-A^{\prime})} \\[0.3em]
\end{bmatrix}
= 12.50 + \\
.1
\begin{bmatrix}
(1000.000000 - 1004.674391) \\[0.3em]
\hline
(1003.235366 - 1004.674391) \\[0.3em]
\end{bmatrix}
\\
\qquad\qquad\qquad\qquad = 12.82483042\%
$$
Step 4:
- First iteration, let I1 =
12.82483042% and repeat Steps 1, 2, and 3
obtaining a new I = .82557859%
- Second iteration, let I1 =
12.82557859% and repeat Steps 1, 2, and 3
obtaining a new I = .82557529%
In this case, no further iterations are required to obtain
the annual percentage rate correct to two decimal places, 12.83%.
(ii) When the iteration
approach is used, it is expected that calculators or computers will
be programmed to carry all available decimals throughout the calculation
and that enough iterations will be performed to make virtually certain
that the annual percentage rate obtained, when rounded to two decimals,
is correct. Annual percentage rates in the examples below were obtained
by using a 10-digit programmable calculator and the iteration procedure
described above.
(1) Single-advance
transaction, with or without an odd first period, and otherwise regular. The general equation in paragraph (b)(8) of this section can be
put in the following special form for this type of transaction:
Figure 5. DISPLAY EQUATION
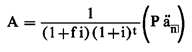
$$
\require{enclose}
\mathrm{A = \frac{1}{(1+fi)(1+i)^t}} \bigg( \mathrm{P\mathrm{\ddot{a}_{\enclose{actuarial}{n}}}} \bigg)
$$
Example (i): Monthly payments
(regular first period)
Amount advanced (A) = $5000. Payment (P)
= $230.
Number of
payments (n) = 24.
Unit period = 1 month. Unit periods per year
(w) = 12.
Advance, 1-10-78. First payment, 2-10-78.
From 1-10-78 through 2-10-78 = 1 unit period. (t = 1;
f = 0)
Annual percentage rate (I) = wi = .0969 = 9.69%
Example (ii): Monthly
payments (long first period)
Amount advanced (A) = $6000. Payment (P) = $200.
Number of payments (n) = 36.
Unit period = 1 month. Unit periods per year (w) = 12.
Advance, 2-10-78. First payment, 4-1-78.
From 3-1-78 through 4-1-78 = 1 unit period. (t = 1)
From 2-10-78 through 3-1-78 = 19 days. (f = 19/30)
Annual percentage rate (I) = wi = .1182 =
11.82%
Example (iii): Semimonthly payments (short first
period)
Amount advanced (A) = $5000. Payment (P) = $219.17.
Number of payments (n) = 24.
Unit period =½ month. Unit periods per year (w) = 24.
Advance, 2-23-78. First payment, 3-1-78. Payments made
on 1st and 16th of each month.
From 2-23-78 through 3-1-78 = 6 days. (t = 0; f = 6/15)
Annual percentage rate (I) = wi = .1034 =
10.34%
Example (iv): Quarterly payments (long first period)
Amount advanced (A) = $10,000. Payment (P) = $385.
Number of payments (n) = 40.
Unit period = 3 months. Unit periods per year (w) = 4.
Advance, 5-23-78. First payment, 10-1-78.
From 7-1-78 through 10-1-78 = 1 unit period. (t = 1)
From 6-1-78 through 7-1-78 = 1 month = 30 days. From 5-23-78
through 6-1-78 = 9 days. (f = 39/90)
Annual percentage rate (I) = wi = .0897 =
8.97%
Example (v): Weekly payments (long first period)
Amount advanced (A) = $500. Payment (P) = $17.60.
Number of payments (n) = 30.
Unit period = 1 week. Unit periods per year (w) = 52.
Advance, 3-20-78. First payment, 4-21-78.
From 3-24-78 through 4-21-78 = 4 unit periods. (t = 4)
From 3-20-78 through 3-24-78 = 4 days. (f = 4/7)
Annual percentage rate (I) = wi = .1496 =
14.96%
(2) Single-advance transaction, with an
odd first payment, with or without an odd first period, and otherwise
regular. The general equation in paragraph (b)(8) of this section
can be put in the following special form for this type of transaction:
Figure 6. DISPLAY EQUATION

$$
\require{enclose}
\mathrm{A} = \frac{1}{(1+\mathrm{fi})(1+\mathrm{i})^\mathrm{t}}
\Bigg[ \mathrm{P}_1 + \frac{\mathrm{P}\ddot{\mathrm{a}}_\enclose{actuarial}{\mathrm{n}-1}}{(1+\mathrm{i})} \Bigg]
$$
Example (i): Monthly payments (regular first period
and irregular first payment)
Amount advanced (A) $5000. First payment (P1) = $250.
Regular payment (P) = $230. Number of payments (n) = 24.
Unit period = 1 month. Unit periods per year (w) = 12.
Advance, 1-10-78. First payment, 2-10-78.
From 1-10-78 through 2-10-78 = 1 unit period. (t = 1;
f = 0)
Annual percentage rate (I) = wi = .1008 =
10.08%
Example (ii): Payments every four weeks (long
first period and irregular first payment)
Amount advanced (A) = $400. First payment (P1) = $39.50.
Regular payment (P) = $38.31. Number of payments (n) =
12.
Unit period = 4 weeks. Unit periods per year (w) = 52/4
= 13.
Advance, 3-18-78. First payment, 4-20-78.
From 3-23-78 through 4-20-78 = 1 unit period. (t = 1)
From 3-18-78 through 3-23-78 = 5 days. (f = 5/28)
Annual percentage rate (I) = wi = .2850 =
28.50%.
(3) Single-advance transaction, with an odd final
payment, with or without an odd first period, and otherwise regular. The general equation in paragraph (b)(8) of this section can be
put in the following special form for this type of transaction:
Figure 7. DISPLAY EQUATION
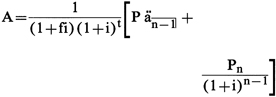
$$
\require{enclose}
\begin{align*}
\mathrm{A} = \frac{1}{(1+\mathrm{fi})(1+\mathrm{i})^\mathrm{t}}
\Bigg[ \mathrm{P}\ddot{\mathrm{a}}_\enclose{actuarial}{\mathrm{n}-1} +&\\
&\frac{\mathrm{P}_\mathrm{n}}{(1+\mathrm{i})^{\mathrm{n}-1}} \Bigg]
\end{align*}
$$
Example (i): Monthly payments (regular first period
and irregular final payment)
Amount advanced (A) = $5000. Regular payment (P) = $230.
Final payment (Pn) = $280. Number of payments
(n) = 24.
Unit period = 1 month. Unit periods per year (w) = 12.
Advance, 1-10-78. First payment, 2-10-78.
From 1-10-78 through 2-10-78 = 1 unit period. (t = 1;
f = 0)
Annual percentage rate (I) = wi = .1050 =
10.50%
Example (ii): Payments every two weeks (short
first period and irregular final payment)
Amount advanced (A) = $200. Regular payment (P) = $9.50.
Final payment (Pn) = $30. Number of payments
(n) = 20.
Unit period = 2 weeks. Unit periods per year (w) = 52/2
= 26.
Advance, 4-3-78. First payment, 4-11-78.
From 4-3-78 through 4-11-78 = 8 days. (t
= 0; f = 8/14)
Annual percentage rate (I) = wi = .1222 =
12.22%
(4) Single-advance transaction, with an odd first
payment, odd final payment, with or without an odd first period, and
otherwise regular. The general equation in paragraph (b)(8) of
this section can be put in the following special form for this type of transaction:
Figure 8. DISPLAY EQUATION
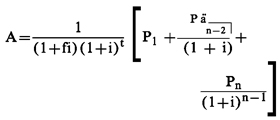
$$
\require{enclose}
\begin{align*}
\mathrm{A = \frac{1}{(1+fi)(1+i)^t}}
\Bigg[ \mathrm{P_1} + &\mathrm{\frac{P\ddot{a}_\enclose{actuarial}{n-2}}{(1+i)}} +\\
&\mathrm{\frac{P_n}{(1+i)^{n-1}}} \Bigg]
\end{align*}
$$
Example (i): Monthly payments
(regular first period, irregular first payment, and irregular final
payment)
Amount advanced (A) = $5000. First payment (P1) = $250.
Regular payment (P) = $230. Final payment (Pn) = $280.
Number of payments (n) = 24. Unit period = 1 month.
Unit periods per year (w) = 12.
Advance, 1-10-78. First payment, 2-10-78.
From 1-10-78 through 2-10-78 = 1 unit period. (t = 1;
f = 0)
Annual percentage rate (I) = wi = .1090 =
10.90%
Example
(ii): Payments every two months (short first period, irregular
first payment, and irregular final payment)
Amount advanced (A) = $8000. First payment (P1) = $449.36.
Regular payment (P) = $465. Final payment (Pn) = $200.
Number of payments (n) = 20. Unit period = 2 months.
Unit periods per year (w) = 12/2 = 6.
Advance, 1-10-78. First payment, 3-1-78.
From 2-1-78 through 3-1-78 = 1 month. From 1-10-78 through
2-1-78 = 22 days. (t = 0; f = 52/60)
Annual percentage rate (I) = wi = .0730 =
7.30%
(5) Single-advance, single-payment transaction. The general equation in paragraph (b)(8) of this section can be
put in the special forms below for single advance, single payment
transactions. Forms 1 through 3 are for the direct determination of
the annual percentage rate under special conditions. Form 4 requires
the use of the iteration procedure of paragraph (b)(9) of this section
and can be used for all single-advance, single-payment transactions
regardless of term.
Form 1—Term less than one year:
Figure 9. DISPLAY EQUATION
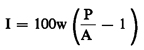
$$
\mathrm{I} = 100\mathrm{w} \Bigg( \mathrm{\frac{P}{A}} -1 \Bigg)
$$
Form 2—Term
more than one year but less than two years:
Figure 10. DISPLAY EQUATION
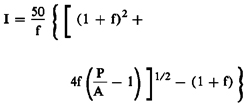
$$
\begin{align*}
\mathrm{I = \frac{50}{f}}
\Bigg\{\Bigg[ & \mathrm{(1+f)^2} + \\[8pt]
& \mathrm{4f} \Bigg( \mathrm{\frac{P}{A} -1} \Bigg) \Bigg]^{1/2} - (1 + \mathrm{f}) \Bigg\}
\end{align*}
$$
Form 3—Term
equal to exactly a year or exact multiple of a year:
Figure 11. DISPLAY EQUATION
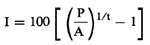
$$
\mathrm{I = 100}
\Bigg[ \Bigg(\mathrm{\frac{P}{A} \Bigg)^{1/\mathrm{t}} -1} \Bigg]
$$
Form 4—Special
form for iteration procedure (no restriction on term):
Figure 12. DISPLAY EQUATION
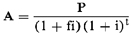
$$
\mathrm{A = \frac{P}{(1+fi)(1+i)^t}}
$$
Example (i): Single-advance,
single-payment (term of less than one year, measured in days)
Amount advanced (A) = $1000. Payment (P) = $1080.
Unit period = 255 days. Unit periods per year (w) = 365/255.
Advance, 1-3-78. Payment, 9-15-78.
From 1-3-78 through 9-15-78 = 255 days. (t = 1; f = 0)
Annual percentage rate (I) = wi = .1145 =
11.45%. (Use form 1 or 4.)
Example (ii): Single-advance,
single-payment (term of less than one year, measured in exact calendar
months)
Amount advanced (A) = $1000. Payment (P) = $1044.
Unit period = 6 months. Unit periods per year (w) = 2.
Advance, 7-15-78. Payment, 1-15-79.
From 7-15-78 through 1-15-79 = 6 mos. (t = 1; f = 0)
Annual percentage rate (I) = wi = .0880 =
8.80%. (Use form 1 or 4.)
Example (iii): Single-advance,
single-payment (term of more than one year but less than two years,
fraction measured in exact months)
Amount advanced (A) = $1000. Payment (P) = $1135.19.
Unit period = 1 year. Unit periods per year (w) = 1.
Advance, 7-17-78. Payment, 1-17-80.
From 1-17-79 through 1-17-80 = 1 unit period. (t = 1)
From 7-17-78 through 1-17-79 = 6 mos. (f = 6/12)
Annual percentage rate (I) = wi = .0876 =
8.76%. (Use form 2 or 4.)
Example (iv): Single-advance,
single-payment (term of exactly two years)
Amount advanced (A) = $1000. Payment (P) = $1240.
Unit period = 1 year. Unit periods per year (w) = 1.
Advance, 1-3-78. Payment, 1-3-80.
From 1-3-78 through 1-3-79 = 1 unit period. (t = 2; f
= 0)
Annual percentage rate (I) = wi = .1136 =
11.36%. (Use form 3 or 4.)
(6) Complex single-advance
transaction.
Example (i): Skipped-payment loan (payments every
four weeks)
A loan of $2135 is advanced on 1-25-78. It is to be repaid
by 24 payments of $100 each. Payments are due every four weeks beginning
2-20-78. However, in those months in which two payments would be due,
only the first of the two payments is made and the following payment
is delayed by two weeks to place it in the next month.
Unit period = 4 weeks. Unit periods per year (w) = 52/4
= 13.
First series of payments begins 26 days after 1-25-78.
(t1 = 0; f1 = 26/28)
Second series of payments begins nine unit periods plus
two weeks after start of first series. (t2 = 10; f2 = 12/28)
Third series of payments begins six unit
periods plus two weeks after start of second series. (t3 = 16; f3 = 26/28)
Last series of payments begins six unit periods plus two
weeks after start of third series. (t4 = 23; f4 = 12/28)
The general equation in paragraph (b)(8) of this section
can be written in the special form:
Figure 13. DISPLAY EQUATION
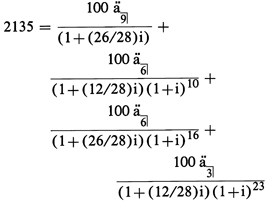
$$
\require{enclose}
\begin{align*}
2135 = & \mathrm{\frac{100\ddot{a}_\enclose{actuarial}{9}}{(1+(26/28)i)} +} \\[8pt]
& \mathrm{\frac{100\ddot{a}_\enclose{actuarial}{6}}{(1+(12/28)i)(1+i)^{10}} + } \\[8pt]
& \mathrm{\frac{100\ddot{a}_\enclose{actuarial}{6}}{(1+(26/28)i)(1+i)^{16}} +} \\[8pt]
& \qquad\qquad \mathrm{\frac{100\ddot{a}_\enclose{actuarial}{3}}{(1+(12/28)i)(1+i)^{23}} } \\
\end{align*}
$$
Annual percentage rate (I) = wi = .1200 =
12.00%
Example
(ii): Skipped-payment loan plus single payments
A loan of $7350 on 3-3-78 is to be repaid by three monthly
payments of $1000 each beginning 9-15-78, plus a single payment of
$2000 on 3-15-79, plus three more monthly payments of $750 each beginning
9-15-79, plus a final payment of $1000 on 2-1-80.
Unit period = 1 month. Unit periods per year (w) = 12.
First series of payments begins six unit periods plus
12 days after 3-3-78. (t1 = 6; f1 = 12/30)
Second series of payments (single payment) occurs 12 unit
periods plus 12 days after 3-3-78. (t2 = 12; f2 = 12/30)
Third series of payments begins 18 unit periods plus 12
days after 3-3-78. (t3 = 18; f3 = 12/30)
Final payment occurs 22 unit periods plus 29
days after 3-3-78. (t4 = 22; f4 = 29/30)
The general equation in paragraph (b)(8) of this section
can be written in the special form:
Figure 14. DISPLAY EQUATION

$$
\require{enclose}
\begin{align*}
7350 = & \mathrm{\frac{1000\ddot{a}_\enclose{actuarial}{3}}{(1+(12/30)i)(1+i)^6} +} \\[8pt]
& \mathrm{\frac{2000}{(1+(12/30)i)(1+i)^{12}} + } \\[8pt]
& \mathrm{\frac{750\ddot{a}_\enclose{actuarial}{3}}{(1+(12/30)i)(1+i)^{18}} +} \\[8pt]
& \qquad\qquad \mathrm{\frac{1000}{(1+(29/30)i)(1+i)^{22}} } \\
\end{align*}
$$
Annual percentage rate
(I) = wi = .1022 = 10.22%
Example (iii): Mortgage with
varying payments
A loan of $39,688.56 (net) on 4-10-78 is to be repaid by 360 monthly
payments beginning 6-1-78. Payments are the same for 12 months at
a time as follows:
Mortgage with
varying payments
| Year |
Monthly payment |
Year |
Monthly payment |
| 1 |
$291.81 |
16 |
$383.67 |
| 2 |
300.18 |
17 |
383.13 |
| 3 |
308.78 |
18 |
382.54 |
| 4 |
317.61 |
19 |
381.90 |
| 5 |
326.65 |
20 |
381.20 |
| 6 |
335.92 |
21 |
380.43 |
| 7 |
345.42 |
22 |
379.60 |
| 8 |
355.15 |
23 |
378.68 |
| 9 |
365.12 |
24 |
377.69 |
| 10 |
375.33 |
25 |
376.60 |
| 11 |
385.76 |
26 |
375.42 |
| 12 |
385.42 |
27 |
374.13 |
| 13 |
385.03 |
28 |
372.72 |
| 14 |
384.62 |
29 |
371.18 |
| 15 |
384.17 |
30 |
369.50 |
Unit period = 1 month. Unit periods per year (w) = 12.
From 5-1-78 through 6-1-78 = 1 unit period. (t = 1)
From 4-10-78 through 5-1-78 = 21 days. (f = 21/30)
The general equation in paragraph (b)(8) of this section
can be written in the special form:
Figure 15. DISPLAY EQUATION
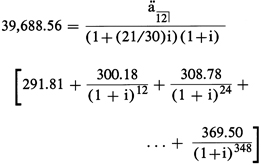
$$
\require{enclose}
\begin{align*}
39&,688.56 = \mathrm{\frac{\ddot{a}_\enclose{actuarial}{12}}{(1+(21/30)i)(1+i)} } \\[8pt]
& \Bigg[291.81 + \frac{300.18}{(1+\mathrm{i})^{12}} + \frac{308.78}{(1+\mathrm{i})^{24}} + \\[8pt]
& \qquad\qquad\qquad\qquad... + \frac{369.50}{(1+\mathrm{i})^{348}} \Bigg]
\end{align*}
$$
Annual percentage rate
(I) = wi = .0980 = 9.80%
(7) Multiple-advance
transactions.
Example (i): Construction loan
Three advances of $20,000 each are made on 4-10-79, 6-12-79,
and 9-18-79. Repayment is by 240 monthly payments of $612.36 each
beginning 12-10-79.
Unit period = 1 month. Unit periods per year
(w) = 12.
From 4-10-79 through 6-12-79 = (2+2/30) unit periods.
From 4-10-79 through 9-18-79 = (5+8/30) unit periods.
From 4-10-79 through 12-10-79 = (8) unit periods.
The general equation in
paragraph (b)(8) of this section is changed to the single-advance
mode by treating the second and third advances as negative payments:
Figure 16. DISPLAY EQUATION
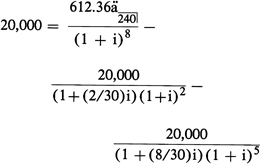
$$
\require{enclose}
\begin{align*}
20,0000 &= \mathrm{\frac{612.36\ddot{a}_{\enclose{actuarial}{240}}}{(1+i)^8} } -\\[8pt]
& \frac{20,000}{(1+(2/30)\mathrm{i})(1+\mathrm{i})^2} - \\[8pt]
& \qquad\qquad \frac{20,000}{(1+(8/30)\mathrm{i}(1+\mathrm{i})^5}
\end{align*}
$$
Annual percentage rate
(I) = wi = .1025 = 10.25%
Example (ii): Student loan
A student loan consists of eight advances: $1800 on 9-5-78,
9-5-79, 9-5-80, and 9-5-81; plus $1000 on 1-5-79, 1-5-80, 1-5-81,
and 1-5-82. The borrower is to make 50 monthly payments of $240 each
beginning 7-1-78 (prior to first advance).
Unit period = 1 month. Unit periods per year (w) = 12.
Zero point is date of first payment since it precedes
first advance.
From 7-1-78 to 9-5-78 = (2+4/30) unit periods.
From 7-1-78 to 9-5-79 = (14+4/30) unit periods.
From 7-1-78 to 9-5-80 = (26+4/30) unit periods.
From 7-1-78 to 9-5-81 = (38+4/30) unit periods.
From 7-1-78 to 1-5-79 = (6+4/30) unit periods.
From 7-1-78 to 1-5-80 = (18+4/30) unit periods.
From 7-1-78 to 1-5-81 = (30+4/30) unit periods.
From 7-1-78 to 1-5-82 = (42+4/30) unit periods.
Since the zero point is
date of first payment, the general equation in paragraph (b)(8) of
this section is written in the single-advance form below by treating
the first payment as a negative advance and the eight advances as
negative payments:
Figure 17. DISPLAY EQUATION
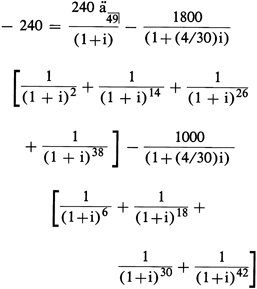
$$
\require{enclose}
\begin{align*}
-&240 = \mathrm{\frac{240\ddot{a}_\enclose{actuarial}{49}}{(1+i)}}
- \mathrm{\frac{1800}{(1+ (4/30)i}} \\[8pt]
& \Bigg[ \mathrm{\frac{1}{(1+i)^2}} + \mathrm{\frac{1}{(1+i)^{14}}} + \mathrm{\frac{1}{(1+i)^{26}}} \\[8pt]
& \qquad + \mathrm{\frac{1}{(1+i)^{38}}} \Bigg] - \mathrm{\frac{1000}{(1+(4/30)i)}} \\[8pt]
& \qquad\qquad \Bigg[ \mathrm{\frac{1}{(1+i)^6}} + \mathrm{\frac{1}{(1+i)^{18}}} + \\[8pt]
& \qquad\qquad\qquad \mathrm{\frac{1}{(1+i)^{30}}} + \mathrm{\frac{1}{(1+i)^{42}}} \Bigg]
\end{align*}
$$
Annual percentage
rate
(I) = wi =
.3204 = 32.04%